e: \(\Leftrightarrow x^3-4x^2+4x-2x^2+2x-x^3+6x^2-6x+2022=0\)
=>0x+2022=0(vô lý)
d)⇔\(\dfrac{4\left(x+1\right)+9\left(2x+1\right)}{12}=\dfrac{2.\left[2x+3\left(x+1\right)\right]+7+12x}{12}\)
⇔\(4\left(x+1\right)+9\left(2x+1\right)=2.\left[2x+3\left(x+1\right)\right]+7+12x\)
⇔4x+4+18x+9=4x+6x+6+7+12x
⇔22x+13=22x+13
⇔0=0 (đúng)
Vậy tập nghiệm của phương trình: S=R
f) Cộng 2 vào các vế của mỗi phương trình:
⇔\(\dfrac{x+1}{2021}+1+\dfrac{x}{2022}+1=\dfrac{x-1}{2023}+1+\dfrac{x-2}{2024}+1\)
⇔\(\dfrac{x+2022}{2021}+\dfrac{x+2022}{2022}=\dfrac{x+2022}{2023}+\dfrac{x+2022}{2024}\)
⇔\(\dfrac{x+2022}{2021}+\dfrac{x+2022}{2022}-\dfrac{x+2022}{2023}-\dfrac{x+2022}{2024}=0\)
⇔(x+2022)(\(\dfrac{1}{2021}+\dfrac{1}{2022}-\dfrac{1}{2023}-\dfrac{1}{2024}\))=0
Vì \(\dfrac{1}{2021}>\dfrac{1}{2023}\);\(\dfrac{1}{2022}>\dfrac{1}{2024}\)=>\(\dfrac{1}{2021}+\dfrac{1}{2022}-\dfrac{1}{2023}-\dfrac{1}{2024}\)>0
Nên phương trình đã cho tương đương:
x+2022=0
⇔x=-2022
Vậy phương trình đã cho có nghiệm duy nhất là x=-2022
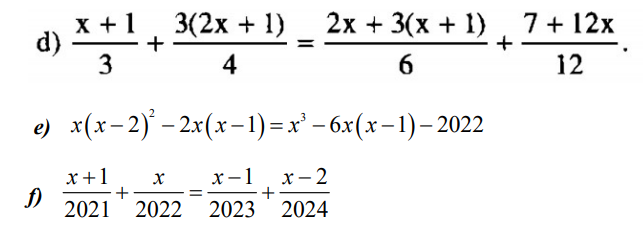
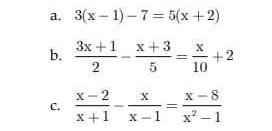
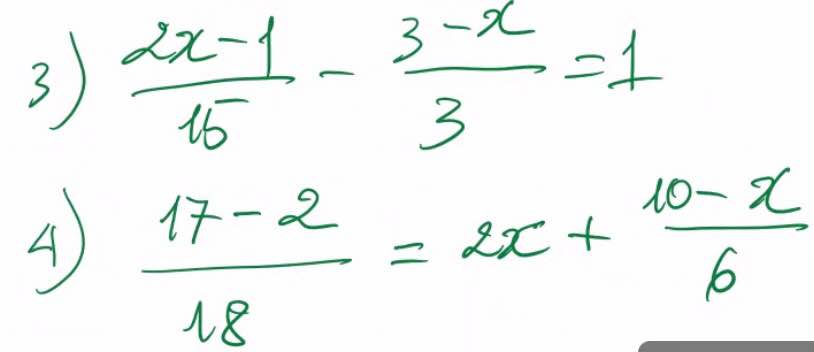
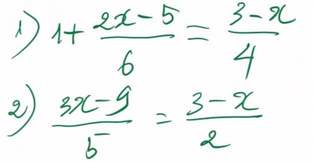
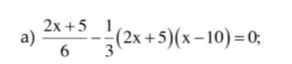
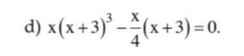
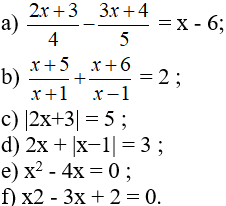
giải các phương trình sau