e. x2-4x=0
<=> x(x-4)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
Vậy phương trình trên có tập nghiệm là: S={0;4}
\(a.\dfrac{2x+3}{4}-\dfrac{3x+4}{5}=x-6\)
\(\Leftrightarrow\dfrac{5\left(2x+3\right)}{20}-\dfrac{4\left(3x+4\right)}{20}=\dfrac{20x}{20}-\dfrac{120}{20}\)
\(\Rightarrow5\left(2x+3\right)-4\left(3x+4\right)=20x-120\)
\(\Leftrightarrow10x+15-12x-16=20x-120\)
\(\Leftrightarrow10x-12x-20x=-120-15+16\)
\(\Leftrightarrow-22x=-119\)
\(\Leftrightarrow x=\dfrac{119}{22}\)
Vậy phương trình có tập nghiệm là: S=\(\left\{\dfrac{119}{22}\right\}\)
f.x2-3x+2=0
<=>x2-x-2x+2=0
<=>x(x-1)-2(x-1)=0
<=>(x-1)(x-2)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là: S={1;2}
\(b.\dfrac{x+5}{x+1}+\dfrac{x+6}{x-1}=2\)
\(\Leftrightarrow\dfrac{\left(x+5\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}+\dfrac{\left(x+6\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{2\left(x+1\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow\left(x+5\right)\left(x-1\right)+\left(x+6\right)\left(x+1\right)=2\left(x+1\right)\left(x-1\right)\)
\(\Leftrightarrow x^2-x+5x-5+x^2+x+6x+6=\left(2x+2\right)\left(x-1\right)\)
\(\Leftrightarrow x^2-x+5x-5+x^2+x+6x+6=2x^2-2x+2x-2\)
\(\Leftrightarrow11x=-3\)
\(\Leftrightarrow x=\dfrac{-3}{11}\)
Vậy phương trình có tập nghiệm là: S=\(\left\{-\dfrac{3}{11}\right\}\)

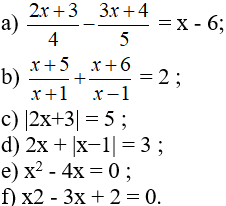






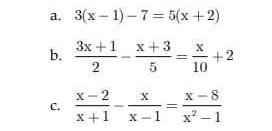

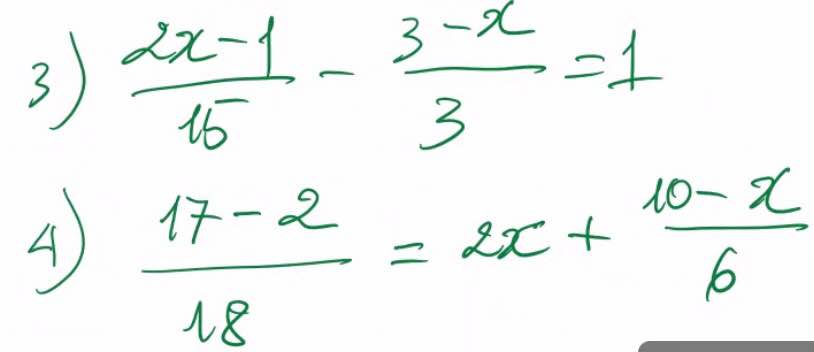

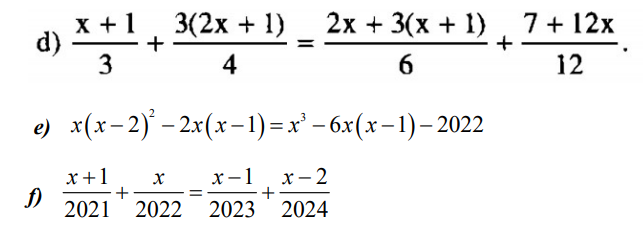
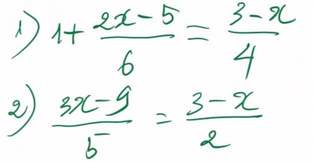

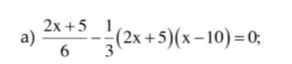


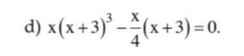

 giải các phương trình sau
giải các phương trình sau