Các câu hỏi tương tự
Diện tích hình phẳng giới hạn bởi các đường
x
−
1
,
x
2
,
y
0
và Parabol
(
P
)
:
y
a
x
2
+
b
x
+
c
bằng 15. Biết (P) có đỉnh I(1;2) là điểm cực tiểu. Khi đó a+b-c bằng bao nhiêu? A. -8 B. -2 C. 14 D. 3
Đọc tiếp
Diện tích hình phẳng giới hạn bởi các đường x = − 1 , x = 2 , y = 0 và Parabol ( P ) : y = a x 2 + b x + c bằng 15. Biết (P) có đỉnh I(1;2) là điểm cực tiểu. Khi đó a+b-c bằng bao nhiêu?
A. -8
B. -2
C. 14
D. 3
Cho parabol
P
1
:
y
-
x
2
+
2
x
+
3
cắt trục hoành tại hai điểm A, B và đường thẳng
d
:
y
a
0
a
4
. Xét parabol
P
2...
Đọc tiếp
Cho parabol P 1 : y = - x 2 + 2 x + 3 cắt trục hoành tại hai điểm A, B và đường thẳng d : y = a 0 < a < 4 . Xét parabol P 2 đi qua A, B và có đỉnh thuộc đường thẳng y = a . Gọi S 1 là diện tích hình phẳng giới hạn bởi P 1 và d. S 2 là diện tích hình phẳng giới hạn bởi P 2 và trục hoành. Biết S 1 = S 2 , tính T = a 3 - 8 a 2 + 48 a .
A. T = 99
B. T = 64
C. T = 32
D. T = 72
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0; x2 có diện tích bằng
28
5
(phần gạch chéo trong hình vẽ). Diện tích hình phẳn...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x=0 có diện tích bằng:

A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x 0; x 2 có diện tích bằng
28
5
(phần gạch chéo tro...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = 0; x = 2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = − 1 ; x = 0 có diện tích bằng:

A. 2 5 .
B. 1 9 .
C. 2 9 .
D. 1 5 .
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C), biết rằng (C) đi qua điểm
A
−
1
;
0
. Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0, x2 bằng...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A − 1 ; 0 . Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0, x=2 bằng 28 5 (phần tô đậm trong hình vẽ).

Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x= -1, x=0 có diện tích bằng
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho parabol (P):
y
x
2
và đường thẳng d đi qua điểm A(1;2). Diện tích hình phẳng giới hạn bởi (C) và d có giá trị nhỏ nhất bằng A.
3
4
B.
1
+
2
2
C.
4
3
D.
2
Đọc tiếp
Cho parabol (P): y = x 2 và đường thẳng d đi qua điểm A(1;2). Diện tích hình phẳng giới hạn bởi (C) và d có giá trị nhỏ nhất bằng
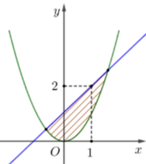
A. 3 4
B. 1 + 2 2
C. 4 3
D. 2
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x0, x2 có diện tích bằng
28
5
(phần gạch chéo trong hình vẽ) A.
2...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0, x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ)
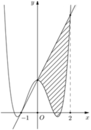
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Kí hiệu S(t) là diện tích của hình phẳng giới hạn bởi các đường y=2x+1, y=0, x=1, x=t (t>1). Tìm t để S(t)=10
A. t=4
C. t=13
C. t=3
D. t=4
Gọi (H) là hình phẳng giới hạn bởi parabol (P):
y
8
x
-
x
2
và trục hoành. Các đường thẳng ya,yb,yc với 0abc16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức
(
16
-
a
)
3
+
(
16
-
b
)
3
+
(
16
-
c...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi parabol (P): y = 8 x - x 2 và trục hoành. Các đường thẳng y=a,y=b,y=c với 0<a<b<c<16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức ( 16 - a ) 3 + ( 16 - b ) 3 + ( 16 - c ) 3 bằng
A. 2048.
B. 3584.
C. 2816.
D. 3480.