Ta có :8!-38308=12
Vậy f(x)=x-38308
Thay x =9!, ta có f(9!)=362880-38308=324572 khác 2072
Vậy đa thức f(x) không tồn tại
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Chứng minh rằng không tồn tại đa thức f(x) có các hệ số nguyên mà f(8!) = 2012 và f(9!) = 2072
Cho đa thức f(x) = ax2 + bx + c. Trong đó a,b,c là các hệ số nguyên. Biết rằng f(x) chia hết cho 3 với mọi \(x\in Z\). Chứng minh rằng a, b, c chia hết cho 3.
Cho đa thức f(x) = ax2 +bx + c. Trong đó a, b, c là các hệ số nguyên. Biết rằng f(x) chia hết cho 3 với mọi \(x\in Z\). Chứng minh a,b,c chia hết cho 3
Chứng minh rằng : Nếu đa thức f(x)=ax + b có hai nghiệm x1 và x2 khác nhau thi f(x) là đa thức 0
Cho hàm số đa thức bậc ba y f (x) có đồ thị đi qua các điểm A(2;4), B(3;9), C(4;16). Các đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các điểm D, E, F (D khác A và B, E khác A và C, F khác B và C). Biết rằng tổng các hoành độ của D, E, F bằng 24. Tính f(0) A.
π
4
B. 0 C.
24
5
D. 2
Đọc tiếp
Cho hàm số đa thức bậc ba y = f (x) có đồ thị đi qua các điểm A(2;4), B(3;9), C(4;16). Các đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các điểm D, E, F (D khác A và B, E khác A và C, F khác B và C). Biết rằng tổng các hoành độ của D, E, F bằng 24. Tính f(0)
A. π 4
B. 0
C. 24 5
D. 2
Cho hàm số đa thức bậc ba y f(x) có đồ thị đi qua các điểm
A
2
;
4
,
B
3
;
9
,
C
4
;
16
. Các đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các điểm D, E, F (D khác A và B; E khác A và C; F khác B và C). Biết rằng tổng các hoành độ của D, E, F bằng 24. Tính ...
Đọc tiếp
Cho hàm số đa thức bậc ba y = f(x) có đồ thị đi qua các điểm A 2 ; 4 , B 3 ; 9 , C 4 ; 16 . Các đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các điểm D, E, F (D khác A và B; E khác A và C; F khác B và C). Biết rằng tổng các hoành độ của D, E, F bằng 24. Tính f 0
A. -2
B. 0
C. 24 5
D. 2
Cho \(f\left(x\right)\) là một đa thức bậc 4. Biết \(f\left(x\right)=f\left(-x\right)\) với mọi \(x\in R\), chứng minh rằng cac hệ số của lũy thừa lẻ đều bằng 0.
Cho hàm số đa thức bậc ba yf(x) có đồ thị của các hàm số yf(x), yf (x)như hình vẽ bên.Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(f(x)-m)+2f(x)3(x+m) có đúng 3 nghiệm thực .Tổng các phần tử của S bằng A. 0 B. -6 C. -7 D. -5
Đọc tiếp
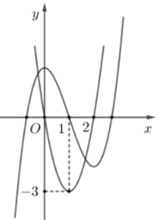
Cho hàm số đa thức bậc ba y=f(x) có đồ thị của các hàm số y=f(x), y=f '(x)như hình vẽ bên.Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(f(x)-m)+2f(x)=3(x+m) có đúng 3 nghiệm thực .Tổng các phần tử của S bằng
A. 0
B. -6
C. -7
D. -5
Cho \(f\left(x\right)\) là một đa thức bậc hai. Biết \(f\left(5\right)=f\left(-5\right)\), chứng minh rằng \(f\left(x\right)=f\left(-x\right)\) với mọi \(x\in R\).
(Toán 7)