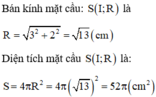Các câu hỏi tương tự
Cho mặt cầu (S) có bán kính R 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu? A.
32
3
c
m
2...
Đọc tiếp
Cho mặt cầu (S) có bán kính R = 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu?
A. 32 3 c m 2
B. 60 3 c m 2
C. 20 3 c m 2
D. 96 3 c m 2
Cho mặt cầu (S) bán kính
R
5
c
m
. Mặt phẳng
P
cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
π
cm
. Bốn điểm A, B, C, D thay đổi sao A, B, C cho thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD. A.
32
3
...
Đọc tiếp
Cho mặt cầu (S) bán kính R = 5 c m . Mặt phẳng P cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π cm . Bốn điểm A, B, C, D thay đổi sao A, B, C cho thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 32 3 c m 3
B. 60 3 c m 3
C. 20 3 c m 3
D. 96 3 c m 3
Cho mặt cầu (S) có tâm I và bán kính R 3. Mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn (C) có chu vi 2ᴨ. Tính khoảng cách d từ tâm I đến mặt phẳng (P). A.
d
2
B.
d
2
2
C.
d
7
2
D.
d
7
Đọc tiếp
Cho mặt cầu (S) có tâm I và bán kính R = 3. Mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn (C) có chu vi 2ᴨ. Tính khoảng cách d từ tâm I đến mặt phẳng (P).
A. d = 2
B. d = 2 2
C. d = 7 2
D. d = 7
Cho mặt cầu (S) bán kính
R
5
c
m
. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
π
(cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S)(D không thuộc đường tròn (C) và tam giác ABC đều. Tính thể tích lớn nhất của tứ diện ABCD. A.
10
3
c
m
3
B.
15...
Đọc tiếp
Cho mặt cầu (S) bán kính R = 5 c m . Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S)(D không thuộc đường tròn (C) và tam giác ABC đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 10 3 c m 3
B. 15 3 c m 3
C. 32 3 c m 3
D. 40 3 c m 3
Cho hình cầu (S) tâm I bán kính R. Một mặt phẳng (P) cắt mặt cầu (S) theo đường tròn giao tuyến (L). Khối nón đỉnh I và đáy là đường tròn (L) có thể tích lớn nhất là
a
π
R
3
b
3
(
a
,
b
∈
N
)
. Hỏi a+b bằng? A. 10 B. 9 C. 11 D. 13
Đọc tiếp
Cho hình cầu (S) tâm I bán kính R. Một mặt phẳng (P) cắt mặt cầu (S) theo đường tròn giao tuyến (L). Khối nón đỉnh I và đáy là đường tròn (L) có thể tích lớn nhất là a π R 3 b 3 ( a , b ∈ N ) . Hỏi a+b bằng?
A. 10
B. 9
C. 11
D. 13
Trong không gian Oxyz cho các mặt phẳng (P): x-y+2z+1 0,(Q):2x+y+z-1 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ đúng một mặt cầu (S) thỏa yêu cầu. A.
r
3
B.
r
2
C.
r...
Đọc tiếp
Trong không gian Oxyz cho các mặt phẳng (P): x-y+2z+1 = 0,(Q):2x+y+z-1 = 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ đúng một mặt cầu (S) thỏa yêu cầu.
A. r = 3
B. r = 2
C. r = 3 2
D. r = 3 2 2
Trong không gian Oxyz cho hai mặt phẳng
P
:
x
-
y
+
2
z
+
1
0
và
Q
:
2
x
+
y
+...
Đọc tiếp
Trong không gian Oxyz cho hai mặt phẳng P : x - y + 2 z + 1 = 0 và Q : 2 x + y + z - 1 = 0 . Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2, (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa mãn yêu cầu.
A. r = 3
B. r = 3 2
C. r = 2
D. r = 3 2 2
Trong không gian Oxyz cho các mặt phẳng
P
:
x
−
y
+
2
z
+
1
0
,
Q
:
2
x
+
y
+
z
−
1
0
Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đư...
Đọc tiếp
Trong không gian Oxyz cho các mặt phẳng P : x − y + 2 z + 1 = 0 , Q : 2 x + y + z − 1 = 0 Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ đúng một mặt cầu (S) thỏa yêu cầu.
A. r = 3 .
B. r = 2 .
C. r = 3 2 .
D. r = 3 2 2 .
Cho hình cầu (S) có tâm I, bán kính bằng 13 cm. Tam giác (T) với độ dài ba cạnh là 27 cm, 29 cm, 52 cm được đặt trong không gian sao cho các cạnh của tam giác tiếp xúc với mặt cầu (S). Khoảng cách từ tâm I đến mặt phẳng chứa tam giác (T) là A. 12 cm. B.
3
2
cm. C. 5 cm. D.
2
3
cm
Đọc tiếp
Cho hình cầu (S) có tâm I, bán kính bằng 13 cm. Tam giác (T) với độ dài ba cạnh là 27 cm, 29 cm, 52 cm được đặt trong không gian sao cho các cạnh của tam giác tiếp xúc với mặt cầu (S). Khoảng cách từ tâm I đến mặt phẳng chứa tam giác (T) là
A. 12 cm.
B. 3 2 cm.
C. 5 cm.
D. 2 3 cm