Các câu hỏi tương tự
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1. Gọi K là trung điểm của DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CK và A′D bằng A.
10
5
B.
4
5
C.
10
10
D.
2
5
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1. Gọi K là trung điểm của DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CK và A′D bằng
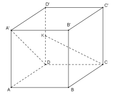
A. 10 5
B. 4 5
C. 10 10
D. 2 5
Cho hình vuông
A
1
B
1
C
1
D
1
có cạnh bằng 1. Gọi
A
k
+
1
,
B
k
+
1
,
C
k
+
1
,
D...
Đọc tiếp
Cho hình vuông A 1 B 1 C 1 D 1 có cạnh bằng 1. Gọi A k + 1 , B k + 1 , C k + 1 , D k + 1 thứ tự là trung điểm các cạnh A k B k , B k C k , C k D k , D k A k (với k = 1,2 ....). Chu vi của hình vuông A 2018 B 2018 C 2018 D 2018 là:
A. 2 2 1007
B. 2 2 1006
C. 2 2 2018
D. 2 2 2017
Cho đa thức K (x) = a+b (x - 1) + c (x - 1). (x - 2)
Tìm a; b; c biết K (1) = 1, K (2) =2; K (0) = 5
Cho hình vuông A1B1C1D1 có cạnh bằng 1. Gọi Ak+1, Bk+1, Ck+1, Dk+1 theo thứ tự là trung điểm của các cạnh AkBk, BkCk, CkDk, DkAk (với
k
1
,
2
,
.
.
.
). Chu vi của hình vuông A2018B2018C2018D2018 bằng A.
2
2...
Đọc tiếp
Cho hình vuông A1B1C1D1 có cạnh bằng 1. Gọi Ak+1, Bk+1, Ck+1, Dk+1 theo thứ tự là trung điểm của các cạnh AkBk, BkCk, CkDk, DkAk (với k = 1 , 2 , . . . ). Chu vi của hình vuông A2018B2018C2018D2018 bằng
A. 2 2 2019
B. 2 2 1006
C. 2 2 2018
D. 2 2 1007
Cho hình vuông
A
1
B
1
C
1
D
1
có cạnh bằng 1. Gọi
A
K
+
1
B
K
+
1
C
K
+
1
D
K
+
1
theo thứ tự là trung...
Đọc tiếp
Cho hình vuông A 1 B 1 C 1 D 1 có cạnh bằng 1. Gọi A K + 1 B K + 1 C K + 1 D K + 1 theo thứ tự là trung điểm của các cạnh A K B K , B K C K , C K D K , D A A K (với K=1,2,...). Chu vi của hình vuông A 2018 B 2018 C 2018 D 2018 bằng
A. 2 2 1007
B. 2 2 1006
C. 2 2 2017
D. 2 2 2018
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy(ABCD). Điểm M thuộc cạnh SA sao cho
S
M
S
A
k
,
0
k
1
Khi đó giá trị của k để mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau là: A.
k
-
1
+...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy(ABCD). Điểm M thuộc cạnh SA sao cho S M S A = k , 0 < k < 1 Khi đó giá trị của k để mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau là:
A. k = - 1 + 5 2
B. k = 1 + 5 4
C. k = - 1 + 5 4
D. k = - 1 + 2 2
1, Cho tg ABC có A90 . Gọi I là TĐ của cạnh AC . Trên tia đối của tia IB lấy điểm D/ IBID. Nối C với D a, CMR tg AIB tg CID b, Gọi M là Tđ Của BC, N là TĐ của AD CMR I là TĐ cuar MN c, Cmr góc AIBBIC Tìm đk tg ABC để AC vuông CD2, Cho tam giác ABC gọi M là TĐ của cạnh BC . Trên tia đối của MA lấy điểm E sao cho MEMA CMR: a,ACBE và AD // BE b, Gọi I là 1 điểm của bk AC, Gọi K là 1 điểm trên BE / AIEK. CMR 3 điểm I,M,K thẳng hàng c, Từ EH vg BC tại H biết HBE50 MEB25 Tính HEM và BME
Đọc tiếp
1, Cho tg ABC có A<90 . Gọi I là TĐ của cạnh AC . Trên tia đối của tia IB lấy điểm D/ IB=ID. Nối C với D a, CMR tg AIB= tg CID b, Gọi M là Tđ Của BC, N là TĐ của AD CMR I là TĐ cuar MN c, Cmr góc AIB<BIC Tìm đk tg ABC để AC vuông CD
2, Cho tam giác ABC gọi M là TĐ của cạnh BC . Trên tia đối của MA lấy điểm E sao cho ME=MA CMR: a,AC=BE và AD // BE b, Gọi I là 1 điểm của bk AC, Gọi K là 1 điểm trên BE / AI=EK. CMR 3 điểm I,M,K thẳng hàng c, Từ EH vg BC tại H biết HBE=50 MEB=25 Tính HEM và BME
Cho hình chóp tứ giác SABCD có đáy ABCD là hình bình hành. Các điểm A, C thỏa mãn
S
A
→
1
3
S
A
,
→
S
C
→
1
5...
Đọc tiếp
Cho hình chóp tứ giác SABCD có đáy ABCD là hình bình hành. Các điểm A', C' thỏa mãn S A ' → = 1 3 S A , → S C ' → = 1 5 S C → . Mặt phẳng (P) chứa đường thẳng A'C' cắt các cạnh SB, SD tại B', D' và đặt k = V S . A ' B ' C ' D ' V S . A B C D . Giá trị nhỏ nhất của k là
A. 4 15
B. 1 30
C. 1 60
D. 15 16
Cho hình bình hành ABCD. Ba đỉnh A, B, C biểu diễn các số phức a = 2 - 2i; b = -1 + i và c = 5 + ki với k ∈ R . Tìm k để ABCD là hình chữ nhật
A. k = 5
B. k = 6
C. k = 7
D. k = 8







