Chọn B.
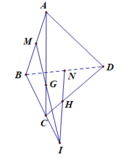
M G ⊂ A B C N H ⊂ B C D A B C ∩ B C D = B C N H ∩ M G = I ⇒ I ∈ B C
vậy B, I, C thẳng hàng
Chọn B.

M G ⊂ A B C N H ⊂ B C D A B C ∩ B C D = B C N H ∩ M G = I ⇒ I ∈ B C
vậy B, I, C thẳng hàng
Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt A B → = b → ; A C → = c → ; A D → = d → . Khẳng định nào sau đây đúng?
A. M P → = 1 2 d → + c → - b →
B. M P → = 1 2 c → + d → + b →
C. M P → = 1 2 c → + b → - d →
D. M P → = 1 2 d → + b → - c →
Cho điểm H(4;0) đường thẳng x = 4 cắt hai đồ thị hàm số y = log a x và y = log b x lần lượt tại 2 điểm A, B sao cho A B = 2 B H . Khẳng định nào sau đây là đúng?
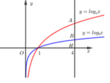
A. b = a 3
B. a = b 3
C. a = 3 b
D. b = 3 a
Cho hình chóp S.ABCD có đáy ABCD là hình thang AB//CD. Gọi I, J lần lượt là trung điểm của các cạnh AD, BC và G là trọng tâm tam giác SAB. Biết thiết diện của hình chóp cắt bởi mặt phẳng (IJG) là hình bình hành. Hỏi khẳng định nào sau đây đúng?
A. AB=3CD
B. A B = 1 3 C D
C. A B = 3 2 C D
D. A B = 2 3 C D
Cho tam giác ABC vuông tại A có AB= 9cm ; BC=10cm
a. Tính AC và so sánh các góc tam giác ABC
b. Trên tia đối tia AB lấy điểm D sao cho A là trung điểm BD. Chứng minh tam giác BCD cân
c. Gọi E; F lần lượt là trung điểm các cạnh DC, BC. Đường thẳng BE cắt cạnh AC tại M.
Tính CM và chứng minh 3 điểm D; M; F thẳng hàng
Trong mặt phẳng Oxy cho B(-1;4), C(3;2). Gọi A là điểm tùy ý sao cho A, B, C không thẳng hàng. Gọi M, N lần lượt là trung điểm của đoạn thẳng AB, và đoạn thẳng AC. Tìm tọa độ của vectơ M N →
A. Không thể xác định vì phụ thuộc vào điểm A.
B. M N → (2;-1)
C. M N → (8;-4)
D. M N → (4;-2)
Cho lăng trụ tam giácABC.A'B'C'. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AC, AA', A' C', BC. Khẳng định nào dưới đây là khẳng định đúng?
A. M N P / / B B ' C ' C
B. N Q P / / A C ' B '
C. M N Q / / A ' B ' C '
D. M P Q / / A A ' B ' B
Cho tứ diện ABCD có M, N lần lượt là trung điểm của các cạnh AC, BC. Điểm P thỏa mãn P B → + 2 P D → = 0 → và điểm Q là giao điểm của hai đường thẳng CD và NP. Hỏi đường thẳng nào sau đây là giao tuyến của hai mp (MNP) và (ACD)?
A. CQ
B. MQ
C. MP
D. NQ
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AD, BC; G là trọng tâm của tam giác BCD. Khi đó, giao điểm của đường thẳng MG và mp (ABC) là:
A. Giao điểm của đường thẳng MG và đường thẳng AN
B. Điểm N
C. Giao điểm của đường thẳng MG và đường thẳng BC
D. Điểm A
Cho a và b là các số thực dương khác 1. Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị y = log a x , y = log b x và trục hoành lần lượt tại A, B và H ta đều có 2 H A = 3 H B (hình vẽ bên). Khẳng định nào sau đây đúng?
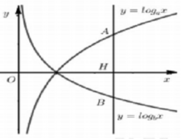
A. a 2 b 3 = 1
B. 3 a = 2 b
C. 2 a = 3 b
D. a 3 b 2 = 1