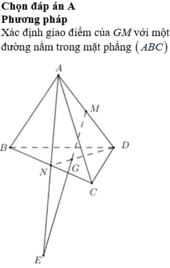
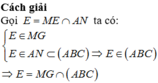Các câu hỏi tương tự
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AD, BC. Gọi G là trọng tâm
∆
B
C
D
Khi đó, giao điểm của đường thẳng MG và mặt phẳng (ABC) là giao điểm của đường thẳng MG và đường thẳng A. BC B. AC C. AN D. AB
Đọc tiếp
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AD, BC. Gọi G là trọng tâm ∆ B C D Khi đó, giao điểm của đường thẳng MG và mặt phẳng (ABC) là giao điểm của đường thẳng MG và đường thẳng
A. BC
B. AC
C. AN
D. AB
Cho tứ diện đều ABCD. Gọi M, N. P lần lượt là trung điểm của các cạnh AB, BC. AD và G là trọng tâm của tam giác BCD. Gọi α là số đo của góc giữa hai đường thẳng MG và NP. Khi đó cosα bằng A.
2
6
B.
2
4
C.
3
6
D.
3
4
Đọc tiếp
Cho tứ diện đều ABCD. Gọi M, N. P lần lượt là trung điểm của các cạnh AB, BC. AD và G là trọng tâm của tam giác BCD. Gọi α là số đo của góc giữa hai đường thẳng MG và NP. Khi đó cosα bằng
A. 2 6
B. 2 4
C. 3 6
D. 3 4
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm AD và AC. Gọi G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng: A. Qua M và song song với AB B. Qua N và song song với BD C. Qua G và song song với CD D. Qua G và song song với BC
Đọc tiếp
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm AD và AC. Gọi G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng:
A. Qua M và song song với AB
B. Qua N và song song với BD
C. Qua G và song song với CD
D. Qua G và song song với BC
Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mặt phẳng (ACD) là A. điểm F B. giao điểm của đường thẳng EG và AC C. giao điểm của đường thẳng EG và CD D. giao điểm của đường thẳng EG và AF
Đọc tiếp
Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mặt phẳng (ACD) là
A. điểm F
B. giao điểm của đường thẳng EG và AC
C. giao điểm của đường thẳng EG và CD
D. giao điểm của đường thẳng EG và AF
Cho tứ diện ABCD có M, N lần lượt là trung điểm của các cạnh AC, BC. Điểm P thỏa mãn
P
B
→
+
2
P
D
→
0
→
và điểm Q là giao điểm của hai đường thẳng CD và NP. Hỏi đường thẳng nào sau đây là giao tuyến của hai mp (MNP) và (ACD)? A. CQ B. MQ C. MP D. NQ
Đọc tiếp
Cho tứ diện ABCD có M, N lần lượt là trung điểm của các cạnh AC, BC. Điểm P thỏa mãn P B → + 2 P D → = 0 → và điểm Q là giao điểm của hai đường thẳng CD và NP. Hỏi đường thẳng nào sau đây là giao tuyến của hai mp (MNP) và (ACD)?
A. CQ
B. MQ
C. MP
D. NQ
Cho tứ diện ABCD, G là trọng tâm của tam giác ABD và M là điểm trên cạnh BC sao cho B M = 2 M C . Đường thẳng MG song song với mặt phẳng
A. (ABC)
B. (BCD)
C. (ABD)
D. (ACD)
Cho hình chóp S.ABC có SASBCACBABa,
S
C
a
3
2
, G là trọng tâm của tam giác ABC. là mặt phẳng đi qua G, song song với các đường thẳng AB và SB. Gọi M, N, P lần lượt là giao điểm của với các đường thẳng BC, AC, SC. Góc giữa hai mặt phẳng (MNP) và (ABC) bằng A. ...
Đọc tiếp
Cho hình chóp S.ABC có SA=SB=CA=CB=AB=a, S C = a 3 2 , G là trọng tâm của tam giác ABC. là mặt phẳng đi qua G, song song với các đường thẳng AB và SB. Gọi M, N, P lần lượt là giao điểm của với các đường thẳng BC, AC, SC. Góc giữa hai mặt phẳng (MNP) và (ABC) bằng
A. 90 0 C
B. 45 0 C
C. 30 0 C
D. 60 0 C
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. M là điểm trên cạnh BC sao cho MB2MC. Khi đó đường thẳng MG song song với mặt phẳng nào dưới đây? A.
(
A
C
D
)
B.
(
B
C
D
)
C.
(
A
B
D
)
D.
(
A
B
C
)
Đọc tiếp
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. M là điểm trên cạnh BC sao cho MB=2MC. Khi đó đường thẳng MG song song với mặt phẳng nào dưới đây?
A. ( A C D )
B. ( B C D )
C. ( A B D )
D. ( A B C )
Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh BC, trên tia đối của tia CB lấy điểm E sao cho CE=BD. Các đường thẳng vuông góc với BC tại D và E lần lượt cắt các đường thẳng AB và Ac theo thứ tự tại M, N. Gọi I là giao điểm của MN với BC. CMR đường thẳng vuông góc với MN luôn đi qua một điểm cố đinh.