Các câu hỏi tương tự
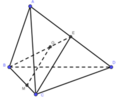
Cho tứ diện ABCD, G là trọng tâm của tam giác ABD và M là điểm trên cạnh BC sao cho B M = 2 M C . Đường thẳng MG song song với mặt phẳng
A. (ABC)
B. (BCD)
C. (ABD)
D. (ACD)
Cho tứ diện ABCD, G là trọng tâm ∆ A B D và M là điểm trên cạnh BC sao cho BM = 2MC. Đường thẳng MG song song với mặt phẳng nào sau đây:
A. (ABC)
B. (ABD)
C. (BCD)
D. (ACD)
Cho tứ diện ABCD, G là trọng tâm ∆ A B D và M là điểm trên cạnh BC sao cho BM = 2MC. Đường thẳng MG song song với mặt phẳng
A. (ACD)
B. (ABC)
C. (ABD)
D. (BCD)
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là điểm thuộc cạnh BC sao cho MB 2MC. Mệnh đề nào sau đây đúng? A.
M
G
|
|
B
C
D
B.
M
G
|
|
A
C
D
C.
M
G...
Đọc tiếp
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là điểm thuộc cạnh BC sao cho MB = 2MC. Mệnh đề nào sau đây đúng?
A. M G | | B C D
B. M G | | A C D
C. M G | | A B D
D. M G | | A B C
Cho hàm số
y
−
x
3
+
3
x
2
+
9
x
có đồ thị (C). Gọi A, B, C, D là bốn điểm trên đồ thị (C) với hoành độ lần lượt là a, b, c, d sao cho tứ giác ABCD là một hình thoi đồng thời hai tiếp tuyến tại A, C song song với nhau và đường thẳng AC tạo với hai trục tọa độ một tam giác cân. Tính tích abcd. A. 144 B. 60 C. 180 D. 120
Đọc tiếp
Cho hàm số y = − x 3 + 3 x 2 + 9 x có đồ thị (C). Gọi A, B, C, D là bốn điểm trên đồ thị (C) với hoành độ lần lượt là a, b, c, d sao cho tứ giác ABCD là một hình thoi đồng thời hai tiếp tuyến tại A, C song song với nhau và đường thẳng AC tạo với hai trục tọa độ một tam giác cân. Tính tích abcd.
A. 144
B. 60
C. 180
D. 120
Trong không gian Oxyz, cho hai điểm A(-3;0;1), B(1;-1;3) và mặt phẳng (P):x - 2y + 2z - 5 0. Đường thẳng (d) đi qua A, song song với mặt phẳng (P) sao cho khoảng cách từ N đến đường thẳng d nhỏ nhất, Đường thẳng (d) có một VTCP là
u
→
(
1
;
b
;
c
)
khi đó
b
c
bằng A.
b
c
11...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(-3;0;1), B(1;-1;3) và mặt phẳng (P):x - 2y + 2z - 5 = 0. Đường thẳng (d) đi qua A, song song với mặt phẳng (P) sao cho khoảng cách từ N đến đường thẳng d nhỏ nhất, Đường thẳng (d) có một VTCP là u → = ( 1 ; b ; c ) khi đó b c bằng
A. b c = 11
B. b c = - 11 2
C. b c = - 3 2
D. b c = 3 2
Cho tam giác ABC, điểm D thuộc cạnh BC. Gọi M là trung điểm của AD. Trên tia đối của tia MB lấy điểm E sao cho ME=MB. Trên tia đối của tia MC lấy điểm F sao cho MF=MC. Chứng minh rằng:
a/ AM=BD
b/ AF song song BC
c/ A,E,F thẳng hàng
Cho tứ diện ABCD. Trên cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho
M
A
A
D
N
C
C
B
1
3
. Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là A. Một hình bình hành B. Một...
Đọc tiếp
Cho tứ diện ABCD. Trên cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho M A A D = N C C B = 1 3 . Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là
A. Một hình bình hành
B. Một hình thang với đáy lớn gấp 2 lần đáy nhỏ
C. Một hình thang với đáy lớn gấp 3 lần đáy nhỏ
D. Một tam giác
Cho tứ diện ABCD. Trên các cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho
M
A
A
D
N
C
C
B
1
3
. Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là A. một tam giác B. một...
Đọc tiếp
Cho tứ diện ABCD. Trên các cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho M A A D = N C C B = 1 3 . Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là
A. một tam giác
B. một hình bình hành
C. Một hình thang với đáy lớn gấp 2 lần đáy nhỏ
D. Một hình thang với đáy lớn gấp 3 lần đáy nhỏ