Các câu hỏi tương tự
Cho hình lập phương ABCD.A’B’C’D’. Tính số đo góc giữa hai mặt phẳng (BA’C) và (DA’C). Tính số đo góc giữa hai mặt phẳng (BA’C) và (DA’C)
A. 60°
B. 135°
C. 150°
D. 90°
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Số đo của góc giữa hai mặt phẳng (BA’C) và (DA’C) là A.
90
0
B.
60
0
C.
30
0
D.
45
0
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Số đo của góc giữa hai mặt phẳng (BA’C) và (DA’C) là
A. 90 0
B. 60 0
C. 30 0
D. 45 0
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Xét M là điểm thay đổi trên cạnh AB. Số đo góc giữa hai đường thẳng AC’ và DM lớn nhất khi độ dài đoạn thẳng AM là
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Xét M là điểm thay đổi trên cạnh AB. Số đo góc giữa hai đường thẳng AC’ và DM lớn nhất khi độ dài đoạn thẳng AM là
![]()
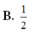
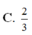
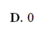
Cho hình lập phương ABCD.A’B’C’D’. Xét (P) là mặt phẳng thay đổi luôn chứa đường thẳng CD’. Giá trị nhỏ nhất của số đo góc giữa mặt phẳng (P) và mặt phẳng (BDD’B’) bằng
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’. Xét (P) là mặt phẳng thay đổi luôn chứa đường thẳng CD’. Giá trị nhỏ nhất của số đo góc giữa mặt phẳng (P) và mặt phẳng (BDD’B’) bằng
![]()
![]()
![]()
![]()
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Bằng phương pháp tọa độ hãy tính khoảng cách giữa hai đường thẳng CA’ và DD’.
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AA' và A'B'. Số đo góc giữa hai đường thẳng MN và BD (như hình vẽ bên) là:
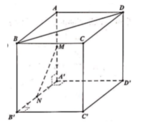
A. 45°.
B. 30°.
C. 60°.
D. 90°.
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy xác định tâm và bán kính mặt cầu:
Đi qua 8 đỉnh của hình lập phương.
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng A’C’ và BD bằng A.
60
0
B.
30
0
C.
45
0
D.
90
0
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng A’C’ và BD bằng
A. 60 0
B. 30 0
C. 45 0
D. 90 0
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy xác định tâm và bán kính mặt cầu:
Tiếp xúc với 6 mặt của hình lập phương.





