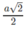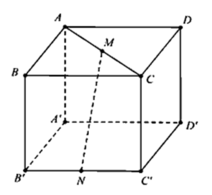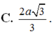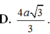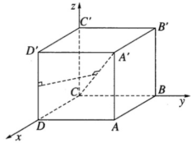
Ta chọn hệ trục tọa độ sao cho: C là gốc tọa độ, CD → = a i → ; CB → = a j → ; CC ' → = a k →
Trong hệ tọa độ vừa chọn ta có: C(0; 0; 0), A’(a; a ; a), D(a; 0; 0), D’(a; 0; a)
CA ' → = (a; a; a), DD ' → = (0; 0; a)
Gọi ( α ) là mặt phẳng chứa CA ' → và song song với DD ' → . Mặt phẳng ( α ) có vecto pháp tuyến là: n → = CA ' → ∧ DD ' → = ( a 2 ; − a 2 ; 0) hay x – y = 0
Phương trình tổng quát của ( α ) là x – y = 0.
Ta có:
d(CA′, DD′) = d(D,(
α
)) = 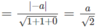
Vậy khoảng cách giữa hai đường thẳng CA’ và DD’ là