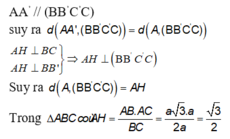Các câu hỏi tương tự
Cho lăng trụ đứng
A
B
C
.
A
B
C
có đáy ABC là tam giác vuông tại B,
A
B
a
,
A
A
2
a
.
Tính khoảng cách từ điểm A đến mặt phẳng
A
B
C
.
A.
2
5...
Đọc tiếp
Cho lăng trụ đứng A B C . A ' B ' C ' có đáy ABC là tam giác vuông tại B, A B = a , A A ' = 2 a . Tính khoảng cách từ điểm A đến mặt phẳng A ' B C .
A. 2 5 a
B. 2 5 a 5
C. 5 a 5
D. 3 5 a 5
Cho lăng trụ đứng
A
B
C
.
A
B
C
có đáy ABC là tam giác vuông tại
B
,
A
B
a
,
A
A
2
a
.
Tính khoảng cách từ điểm A đến mặt phẳng
(
A
B
C
)
.
A.
2
5
a...
Đọc tiếp
Cho lăng trụ đứng A B C . A ' B ' C ' có đáy ABC là tam giác vuông tại B , A B = a , A A ' = 2 a . Tính khoảng cách từ điểm A đến mặt phẳng ( A ' B C ) .
A. 2 5 a
B. 2 5 a 5
C. 5 a 5
D. 3 5 a 5
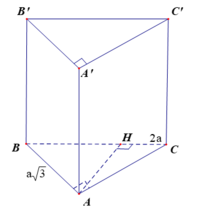
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông tại A,AB
a
3
,ACAAa. Sin góc giữa đường thẳng AC′ và mặt phẳng (BCC′B′) bằng A.
3
3
B.
10
4
C.
10
4
D.
6
4
Đọc tiếp
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông tại A,AB= a 3 ,AC=AA'=a. Sin góc giữa đường thẳng AC′ và mặt phẳng (BCC′B′) bằng
A. 3 3
B. 10 4
C. 10 4
D. 6 4
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông tại B, AB a, AA 2a. Gọi M là trung điểm của đoạn thẳng AC, I là giao điểm của AM và AC. Tính khoảng cách từ điểm A đến mặt phẳng (IBC). A.
2
5
a
5
.
B.
5
a
5
....
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AB = a, AA' = 2a. Gọi M là trung điểm của đoạn thẳng A'C', I là giao điểm của AM và A'C. Tính khoảng cách từ điểm A đến mặt phẳng (IBC).
A. 2 5 a 5 .
B. 5 a 5 .
C. 2 3 a 5 .
D. 3 a 5 .
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của A’ lên mặt phẳng (ABC) trùng với tâm G của tam giác ABC. Biết khoảng cách giữa AA’ và BC là
a
3
4
. Khoảng cách từ điểm A’ đến mặt phẳng bằng: A. a/3 B.
a
165
55
C. 3/a D.
a...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của A’ lên mặt phẳng (ABC) trùng với tâm G của tam giác ABC. Biết khoảng cách giữa AA’ và BC là a 3 4 . Khoảng cách từ điểm A’ đến mặt phẳng bằng:
A. a/3
B. a 165 55
C. 3/a
D. a 3 6
Cho hình lăng trụ đứng ABC.A B C có đáy là tam giác vuông cân đỉnh A, BC2a, thể tích khối lăng trụ đã cho bằng
a
3
. Khoảng cách từ điểm B đến mặt phẳng (A BC) bằng A.
2
a
B.
6
a
4
. C.
2...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A' B' C' có đáy là tam giác vuông cân đỉnh A, BC=2a, thể tích khối lăng trụ đã cho bằng a 3 . Khoảng cách từ điểm B' đến mặt phẳng (A' BC) bằng
A. 2 a B. 6 a 4 . C. 2 a 2 . D. 6 a 3
B. 6 a 4 .
C. 2 a 2 .
Cho lăng trụ
A
B
C
.
A
B
C
có đáy
A
B
C
là tam giác vuông cân tại
A
,
B
C
2
2
a
.
Hình chiếu vuông góc của
A
lên mặt phẳng
A
B
C
trùng với trung điểm O của BC. Khoảng các...
Đọc tiếp
Cho lăng trụ A B C . A ' B ' C ' có đáy A B C là tam giác vuông cân tại A , B C = 2 2 a . Hình chiếu vuông góc của A ' lên mặt phẳng A B C trùng với trung điểm O của BC. Khoảng cách từ O đến A A ' bằng 3 2 a 11 . Tính thể tích của khối lăng trụ đã cho
A. 6 3 a 3
B. 6 a 3
C. 2 a 3
D. 12 2 a 3
Cho hình lăng trụ đứng ABC ABC Cạnh bên AAa, ABC là tam giác vuông tại A có
B
C
2
a
,
A
B
a
3
.
Tính khoảng cách từ đỉnh A đến mặt phẳng
A
B
C
.
A.
a
21
7
.
B....
Đọc tiếp
Cho hình lăng trụ đứng ABC A'B'C' Cạnh bên AA'=a, ABC là tam giác vuông tại A có B C = 2 a , A B = a 3 . Tính khoảng cách từ đỉnh A đến mặt phẳng A ' B C .
A. a 21 7 .
B. a 21 21 .
C. a 3 2 12 .
D. a 7 21 .
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là các tam giác đều cạnh bằng 1,
A
A
3
. Tính khoảng cách d từ điểm A đến mặt phẳng (A’BC) A.
d
2
15
5
B.
d
15
5
C.
d
3
2
D. ...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là các tam giác đều cạnh bằng 1, A A ' = 3 . Tính khoảng cách d từ điểm A đến mặt phẳng (A’BC)
A. d = 2 15 5
B. d = 15 5
C. d = 3 2
D. d = 3 4