Gọi x là độ dài cạnh đáy của chóp đều S.ABCD .
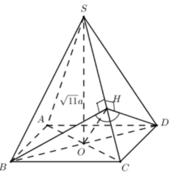
Gọi
![]()
Ta có:

Ta có:
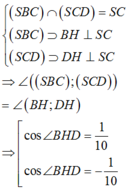
Dễ dàng chứng minh được

cân tại H.
Xét tam giác SBC ta có:

Xét tam giác BDH có:
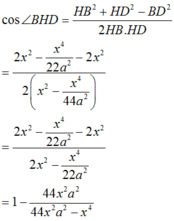
TH1:
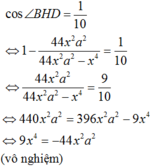
TH2:

Xét tam giác vuông SOA có:
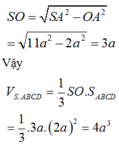
Chọn C.
Gọi x là độ dài cạnh đáy của chóp đều S.ABCD .

Gọi
![]()
Ta có:

Ta có:
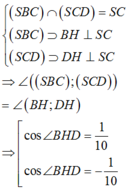
Dễ dàng chứng minh được

cân tại H.
Xét tam giác SBC ta có:

Xét tam giác BDH có:
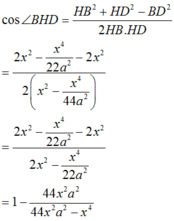
TH1:
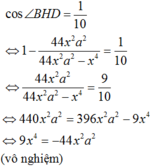
TH2:

Xét tam giác vuông SOA có:
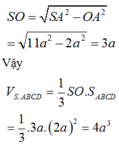
Chọn C.
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B với AB = BC = a,
AD = 2a. Biết SA vuông góc với mặt phằng (ABCD) và S A = a 5 . Côsin của góc tạo bởi hai mặt phẳng (SBC) và (SCD) bằng
A. 2 21 21 .
B. 21 12 .
C. 21 6 .
D. 21 21 .
Cho hình chóp S . A B C D có đáy ABCD là tứ giác lồi và góc tạo bởi các mặt phẳng ( S A B ) , ( S B C ) , ( S C D ) , ( S D A ) với mặt đáy lần lượt là 90 ° , 60 ° , 60 ° , 60 ° . Biết rằng tam giác SAB vuông cân tại S , A B = a và chu vi tứ giác ABCD là 9a. Tính thể tích V của khối chóp S . A B C D ?
A. V = a 3 3 4
B. V = a 3 3
C. V = 2 a 3 3 9
D. V = a 3 3 9
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD). Biết góc tạo bởi mặt phẳng (SCD) và đáy bằng 30 0 và khoảng cách từ A tới mặt phẳng (SCD) bằng a. Khi đó thể tích V của khối chóp S.ABCD bằng bao nhiêu?
A. 8 3 a 3 3 .
B. 2 3 a 3 3 .
C. 4 3 a 3 9 .
D. 8 3 a 3 9 .
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
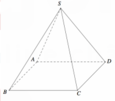
A. 3 3
B. 1 2
C. 3 2
D. 3 6
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
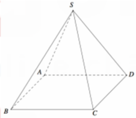
A. 3 3
B. 1 2
C. 3 2
D. 3 6
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB = a. Biết SA = a và vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (SCD) bằng φ , với cos φ = 2 5 . Tính theo a thể tích của khối chóp S.ABCD
A. 4 3 a 3
B. 2 3 a 3
C. 2 a 3
D. a 3 3
Cho hình chóp đều S.ABCD có A C = 2 a ; góc giữa mặt phẳng S B C và mặt phẳng A B C D bằng 45 ° . Tính thể tích V của khối chóp S.ABCD theo a.
A. V = a 3 2 3
B. V = 2 3 a 3 3
C. V = a 3 2
D. V = a 3 2
Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng a và thể tích khối chóp bằng a 3 2 6 . Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBC)
A. a 6 3 .
B. a 6 3 .
C. a 6 6 .
D. a 6 .
Cho khối chóp tứ giác S.ABCD có đáy là hình bình hành, AD=4a, SA=SB=SC=SD= 6 a . Khi khối chóp S.ABCD có thể tích đạt giá trị lớn nhất, sin của góc giữa hai mặt phẳng (SBC) và (SCD) bằng
A. 6 6
B. 15 5
C. 5 5
D. 3 3