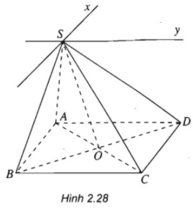
a)
Ta có:
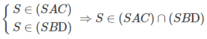
Giả sử:
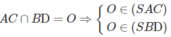
⇒ O ∈ (SAC) ∩ (SBD)
⇒ (SAC) ∩ (SBD) = SO
b) Ta có:
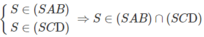
Ta lại có
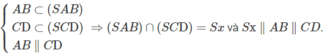
c) Lập luận tương tự câu b) ta có ⇒ (SAD) ∩ (SBC) = Sy và Sy // AD // BC.

a)
Ta có:
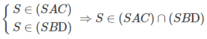
Giả sử:
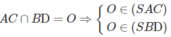
⇒ O ∈ (SAC) ∩ (SBD)
⇒ (SAC) ∩ (SBD) = SO
b) Ta có:
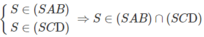
Ta lại có
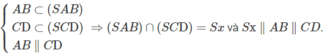
c) Lập luận tương tự câu b) ta có ⇒ (SAD) ∩ (SBC) = Sy và Sy // AD // BC.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trung điểm của CD là M. Tìm giao tuyến của các mặt phẳng sau đây:
a) (SAC) và (SBD) b) (SBM) và (SAC)
c) (SBM) và (SAD) d) (SAM) và (SBC)
cho hình chóp S.ABCD đáy ABCD là tứ giác lồi (các cặp cạnh đối không song song. Gọi E là điểm thuộc cạnh SC
a) tìm giao tuyến của 2 mặt phẳng (SAC) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật tâm O. Gọi H,K lần lượt là trung điểm SA,SB
a) tìm giao tuyến của hai mặt phẳng (SBD) và (SAC)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
d) tìm giao tuyến của 2 mặt phẳng (HKCD) và (ABCD)
cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật tâm O. Gọi H,K lần lượt là trung điểm SA,SB
a) tìm giao tuyến của 2 mặt phẳng (SBD) và (SAC)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
d) tìm giao tuyến của 2 mặt phẳng (HKCD) và (ABCD)
1) cho hình chóp S.ABCD đáy ABCD là hình chữ nhật, tâm O. Điểm H thuộc cạnh SC
a) tìm giao tuyến của 2 mặt phẳng (SAC) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SAD)
c) tìm giao tuyến của 2 mặt phẳng (HAD) và (SCD)
2) cho hình chóp S.ABCD đáy ABCD là hình vuông, tâm I. Điểm K thuộc cạnh SD, vẽ hình
a) tìm giao tuyến của 2 mặt phẳng (SAC) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SCD) và (SAD)
c) tìm giao tuyến của 2 mặt phẳng (KAB) và (SAD)
cho hình chóp S.ABCD, đáy ABCD là vuông tâm I. Gọi M,N lần lượt là trung điểm SB,SC
a) tìm giao tuyến của hai mặt phẳng (SBD) và (SAC)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
d) tìm giao tuyến của 2 mặt phẳng (MNA) và (ABCD)
cho hình chóp S.ABCD đáy ABCD là hình chữ nhật, tâm O. Điểm H thuộc cạnh SC
a) tìm giao tuyến của 2 mặt phẳng (SAC) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SAD)
c) tìm giao tuyến của 2 mặt phẳng (HAD) và (SCD)
Cho hình chóp S.ABCD, đáy ABCD là hình thang AB // CD , AB > CD. Tìm giao tuyến của các mặt phẳng.
a)(SAC) và (SBD)
b)(SAD) và (SBC)
c)(SAB) và (SCD)
d) gọi M là trung điểm của SA, (P) là mặt phẳng đi qua M, (P) song song với AB và AD. Tìm giao tuyến của (P) với mặt phẳng (SAB) và (SAD) với AB và AD. Tìm giao tuyến của (P) với mặt phẳng (SAB) và (SAD)
Cho hình chóp S.ABCD, có đáy ABCD là hình thang có đáy lớn AD . Gọi E, F lần lượt là trung điểm của SA, SD.
a) Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (SBD), (SAD) và (SBC).
b) Chứng minh EF// (ABCD) và EF// (SBC)
c) Gọi K là giao điểm của AB và CD. Tìm M, N lần lượt là giao điểm của SB và (CDE); SC và (EFM). Từ đó, tìm thiết diện của hình chóp cắt bởi mặt phẳng (KEF)
d) Cho AD=2BC. Tính tỉ số diện tích của tam giác KMN và tam giác KEF .
giúp mình giải câu d với ạ