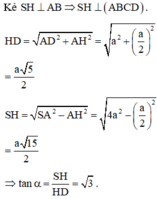Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S có SASB2a nằm trong mặt phẳng vuông góc với đáy ABCD. Gọi α là góc giữa SD và mặt phẳng đáy (ABCD). Mệnh đề nào sau đây đúng A.
tan
α
3
B.
c
o
t
α
3
6
C.
tan
α
3
3
D.
c...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S có SA=SB=2a nằm trong mặt phẳng vuông góc với đáy ABCD. Gọi α là góc giữa SD và mặt phẳng đáy (ABCD). Mệnh đề nào sau đây đúng
A. tan α = 3
B. c o t α = 3 6
C. tan α = 3 3
D. c o t α = 2 3
Cho hình chóp
S
.
A
B
C
D
có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng
A
B
C
D
là trung điểm H của đoạn OA và
S
D
,
A
B
C...
Đọc tiếp
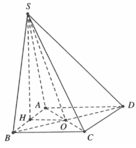
Cho hình chóp S . A B C D có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng A B C D là trung điểm H của đoạn OA và S D , A B C D = 60 ∘ . Gọi α là góc giữa hai mặt phẳng S C D v à A B C D . Tính t a n α .
A. t a n α = 4 15 9
B. tan α = 30 12
C. tan α = 10 3
D. tan α = 30 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hình chiếu vuông góc của đỉnh S xuống mặt đáy nằm trong hình vuông ABCD. Hai mặt phẳng (SAD), (SBC) vuông góc với nhau; góc giữa hai mặt phẳng
S
A
B
v
à
S
A
C
là
60
°
;
góc giữa hai mặt phẳng
S
A
B...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hình chiếu vuông góc của đỉnh S xuống mặt đáy nằm trong hình vuông ABCD. Hai mặt phẳng (SAD), (SBC) vuông góc với nhau; góc giữa hai mặt phẳng S A B v à S A C là 60 ° ; góc giữa hai mặt phẳng S A B v à S A D là 45 ° Gọi α là góc giữa hai mặt phẳng S A B v à A B C D , tính cos α
A. cos α = 1 2
B. cos α = 2 2
C. cos α = 3 2
D. cos α = 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
α
là góc tạo bởi đường thẳng BD với (SAD). Tính
sin
α
? A.
2
3
B.
1
2
C.
6
4
D.
10
4
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi α là góc tạo bởi đường thẳng BD với (SAD). Tính sin α ?
A. 2 3
B. 1 2
C. 6 4
D. 10 4
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD). Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng
α
với
tan
α
10
5
. Tính góc giữa đường thẳng SO và mặt phẳng (ABCD). A.
60
°
B.
69
,
3
°
C.
90
°
D.
45
°
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD). Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng α với tan α = 10 5 . Tính góc giữa đường thẳng SO và mặt phẳng (ABCD).
A. 60 °
B. 69 , 3 °
C. 90 °
D. 45 °
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a,
S
A
⊥
(
A
B
C
D
)
và
S
A
3
. Gọi
α
là góc tạo bởi giữa đường thẳng SB và mặt phẳng (SAC), khi đó
α
thỏa mãn hệ thức nào sau đây? A.
cos
α
2
8
B.
sin...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, S A ⊥ ( A B C D ) và S A = 3 . Gọi α là góc tạo bởi giữa đường thẳng SB và mặt phẳng (SAC), khi đó α thỏa mãn hệ thức nào sau đây?
A. cos α = 2 8
B. sin α = 2 8
C. sin α = 2 4
D. cos α = 2 4
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc vói đáy. Gọi M là trung điểm của SC và α là số đo của góc giữa hai đường thẳng AC, BM. Khi đó cosα bằng A.
3
6
B.
6
3
C.
2
3
D.
2
6
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc vói đáy. Gọi M là trung điểm của SC và α là số đo của góc giữa hai đường thẳng AC, BM. Khi đó cosα bằng
A. 3 6
B. 6 3
C. 2 3
D. 2 6
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AD 2cm, DC 1cm,
ADC
^
120
0
. Cạnh bên SB
3
cm, hai mặt phẳng (SAB) và (SBC) cùng vuông góc với mặt phẳng đáy. Gọi
α
là góc tạo bởi SD và mặt phẳng (SAC). Tính A.
sinα
1
4
B.
sinα...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AD = 2cm, DC = 1cm, ADC ^ = 120 0 . Cạnh bên SB= 3 cm, hai mặt phẳng (SAB) và (SBC) cùng vuông góc với mặt phẳng đáy. Gọi α là góc tạo bởi SD và mặt phẳng (SAC). Tính
A. sinα = 1 4
B. sinα = 3 7
C. sinα = 3 4
D. sinα = 3 4
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của đoạn OA và
S
D
,
A
B
C
D
^
60
0
. Gọi...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của đoạn OA và S D , A B C D ^ = 60 0 . Gọi α là góc giữa hai mặt phẳng (SCD) và (ABCD). Tính tan α .
A. tan α = 4 15 9 .
B. tan α = 30 12 .
C. tan α = 10 3 .