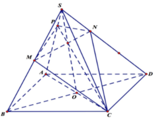
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có thể tích là V. Gọi M là một điểm trên cạnh AB sao cho M A A B = x , 0 < x < 1 . Biết rằng mặt phẳng α qua M và song song với (SBC) chia khối chóp S.ABCD thành hai phần trong đó phần chứa điểm A thể tích bằng 4 27 V . Tính giá trị của biểu thức P = 1 − x 1 + x
A. 1/2
B. 1/5
C. 1/3
D. 3/5
Đáp án A

Kẻ M N ∥ B C N ∈ C D , N P ∥ S C P D , M Q ∥ S B Q ∈ S A
⇒ m p a cắt khối chóp S.ABCD theo thiết diện là MNPQ
Ta có M A A B = A Q S A = N D C D = x ⇒ S Q S A = S P S D = 1 − x (Định lý Thalet)
Mà Δ A M N = Δ A D N ⇒ V Q . A M N = V P . A D N = x V S . A M N = x 2 V S . A M N D = x 2 2 V
Và S N . A P Q = 1 3 d N ; S A D . S Δ A P Q = x 1 − x × V N . S A D = x 2 1 − x 2 V
Do đó V A Q M . D P N = V Q . A M N + V P . A N D + V N . A P Q = 3 x 2 − x 3 2 × V = 4 27 V
. ⇒ x 3 − 3 x 2 + 8 27 = 0 ⇒ x = 1 3 Vậy P = 1 − x 1 + x x = 1 3 = 1 2