a.
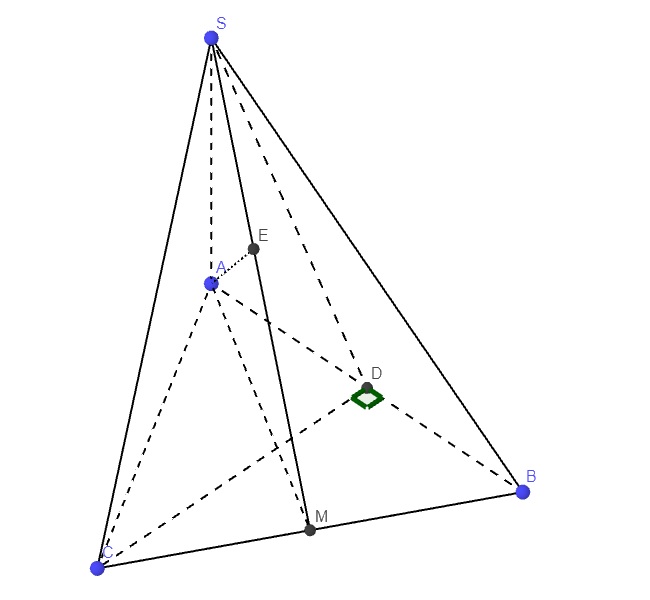
Gọi D là trung điểm AB \(\Rightarrow CD\perp AB\) (tam giác đều)
\(SA\perp\left(ABC\right)\Rightarrow SA\perp CD\)
\(\Rightarrow CD\perp\left(SAB\right)\Rightarrow\widehat{CSD}\) là góc giữa SC và (SAB)
\(CD=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(SD=\sqrt{SA^2-AD^2}=\sqrt{\left(2a\right)^2-\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{15}}{2}\)
\(tan\widehat{CSD}=\dfrac{CD}{SD}=\dfrac{\sqrt{5}}{5}\Rightarrow\widehat{CSD}\approx24^06'\)
b.
\(AM\perp BC\) (t/c tam giác đều)
\(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\Rightarrow BC\perp\left(SAM\right)\)
Từ A kẻ \(AE\perp SM\Rightarrow AE\perp\left(SBC\right)\)
\(\Rightarrow\widehat{AME}\) hay \(\widehat{AMS}\) là góc giữa AM và (SBC)
\(AM=\dfrac{a\sqrt{3}}{2}\Rightarrow tan\widehat{AMS}=\dfrac{SA}{AM}=\dfrac{4\sqrt{3}}{3}\)
\(\Rightarrow\widehat{AMS}\approx66^035'\)
c.
Đề bài có vấn đề, M thuộc BC nên (SCM) trùng (SBC), mà SB cũng thuộc (SBC) luôn, do đó góc bằng 0