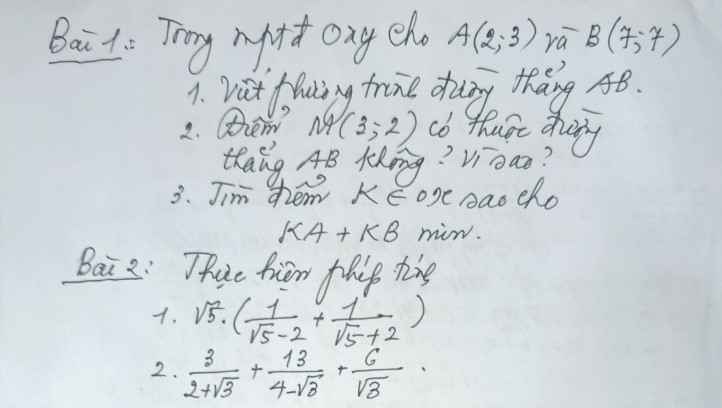Question

Cho hệ phương trình \(\left\{{}\begin{matrix}3x-y=2m-1\\x+2y=3m+2\end{matrix}\right.\)      (với m là tham số)

Tìm m để hệ đã cho có nghiệm (x;y) thỏa mãn: x² + y² + 3 đạt giá trị nhỏ nhất.

Answer 1

\(\left\{{}\begin{matrix}3x-y=2m-1\\x+2y=3m+2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}6x-2y=4m-2\\x+2y=3m+2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}6x-2y+x+2y=4m-2+3m+2\\x+2y=3m+2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}7x=7m\\x+2y=3m+2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\m+2y=3m+2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\2y=2m+2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=m+1\end{matrix}\right.\)

\(x^2+y^2+3\\ =m^2+\left(m+1\right)^2+3\\ =m^2+m^2+2m+1+3\\ =2m^2+2m+4\\ =2\left(m^2+m+2\right)\)

\(=2\left(m^2+m+\dfrac{1}{4}+\dfrac{7}{4}\right)\)

\(=2\left[\left(m+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\right]\)

\(=2\left(m+\dfrac{1}{2}\right)^2+\dfrac{7}{2}\ge\dfrac{7}{2}\)

Dấu "=" xảy ra \(\Leftrightarrow m=-\dfrac{1}{2}\)

Vậy ...