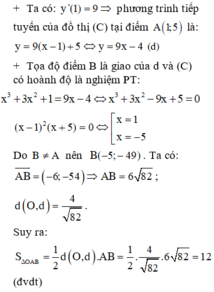Các câu hỏi tương tự
Cho hàm số:
y
x
3
-
6
x
2
+
9
x
-
2
có đồ thị là (C). Biết d là phương trình tiếp tuyến của đồ thị (C) tại điểm
A
1
;
5
. Gọi B là giao điểm của tiếp tuyến với đồ thị (C). Diện tích...
Đọc tiếp
Cho hàm số: y = x 3 - 6 x 2 + 9 x - 2 có đồ thị là (C). Biết d là phương trình tiếp tuyến của đồ thị (C) tại điểm A 1 ; 5 . Gọi B là giao điểm của tiếp tuyến với đồ thị (C). Diện tích tam giác OAB, với O là gốc tọa độ là bao nhiêu:
Chọn đáp án đúng:
Cho hàm số
y
x
+
2
2
x
+
3
có đồ thị (C). Đường thẳng (d) có phương trình
y
a
x
+
b
là tiếp tuyến của (C), biết (d) cắt trục hoành tại A và cắt trục tung tại B sao cho tam giác OAB cân tại O, với O là gốc tọa độ. Tính a+ b A. 0 B. -2 C. -1 D. -3
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Đường thẳng (d) có phương trình y = a x + b là tiếp tuyến của (C), biết (d) cắt trục hoành tại A và cắt trục tung tại B sao cho tam giác OAB cân tại O, với O là gốc tọa độ. Tính a+ b
A. 0
B. -2
C. -1
D. -3
Cho hàm số
y
x
+
2
2
x
+
3
có đồ thị (C). Đường thẳng d có phương trình
y
a
x
+
b
là tiếp tuyến của (C), biết d cắt trục hoành tại A và cắt trục tung tại B sao cho tam giác OAB cân tại O, với O là gốc tọa độ. Tính a+b A. -1 B. -2 C. 0 D. -3
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Đường thẳng d có phương trình y = a x + b là tiếp tuyến của (C), biết d cắt trục hoành tại A và cắt trục tung tại B sao cho tam giác OAB cân tại O, với O là gốc tọa độ. Tính a+b
A. -1
B. -2
C. 0
D. -3
Phương trình tiếp tuyến của đồ thị hàm số
y
2
x
-
1
x
-
3
(
C
)
tại M(4;7) cắt hai trục tọa độ tại A, B. Diện tích của tam giác OAB là (O là gốc tọa độ): A.
729
2
B.
729
5
C.
729
D.
729
10
Đọc tiếp
Phương trình tiếp tuyến của đồ thị hàm số y = 2 x - 1 x - 3 ( C ) tại M(4;7) cắt hai trục tọa độ tại A, B. Diện tích của tam giác OAB là (O là gốc tọa độ):
A. 729 2
B. 729 5
C. 729
D. 729 10
Cho hàm số
y
x
3
+
3
x
2
−
1
có đồ thị (C). Gọi Δ là tiếp tuyến của (C) tại điểm có hoành độ
x
0
0
, B là giao điểm thứ hai của Δ với (C). Tính diện tích tam giác OAB. A.
1
4
. B.
3
2
. C....
Đọc tiếp
Cho hàm số y = x 3 + 3 x 2 − 1 có đồ thị (C). Gọi Δ là tiếp tuyến của (C) tại điểm có hoành độ x 0 = 0 , B là giao điểm thứ hai của Δ với (C). Tính diện tích tam giác OAB.
A. 1 4 .
B. 3 2 .
C. 1 2 .
D. 2.
Cho hàm số
y
x
x
−
1
có đồ thị
C
và đường thẳng
d
:
y
−
x
+
m
.
Khi đó số giá trị của m để đường thẳng d cắt đồ thị
C
tại hai điểm phân biệt A, B sao cho tam giác OAB (O là gốc tọa độ ) có bán kính đường tròn ngoại tiếp bằng
2...
Đọc tiếp
Cho hàm số y = x x − 1 có đồ thị = C và đường thẳng d : y = − x + m . Khi đó số giá trị của m để đường thẳng d cắt đồ thị C tại hai điểm phân biệt A, B sao cho tam giác OAB (O là gốc tọa độ ) có bán kính đường tròn ngoại tiếp bằng 2 2 là:
A.0
B. 3
C. 1
D. 2
Cho hàm số
y
x
+
2
2
x
+
3
có đồ thị (C). Giả sử, đường thẳng d: ykx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. Tổng k+m có giá trị bằng: A. 1. B. 3. C. -1 D. -3
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Giả sử, đường thẳng d: y=kx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. Tổng k+m có giá trị bằng:
A. 1.
B. 3.
C. -1
D. -3
Biết điểm A có hoành độ lớn hơn – 4 là giao điểm của đường thẳng
y
x
+
7
với đồ thị (C) của hàm số
y
2
x
-
1
x
+
1
. Tiếp tuyến của đồ thì (C) tại điểm A cắt hai trục độ Ox, Oy lần lượt tịa E, F. Khi đó tam giác OEF (O là gốc tạo độ) có diện tích bằng: A. ...
Đọc tiếp
Biết điểm A có hoành độ lớn hơn – 4 là giao điểm của đường thẳng y = x + 7 với đồ thị (C) của hàm số y = 2 x - 1 x + 1 . Tiếp tuyến của đồ thì (C) tại điểm A cắt hai trục độ Ox, Oy lần lượt tịa E, F. Khi đó tam giác OEF (O là gốc tạo độ) có diện tích bằng:
A. 33 2
B. 121 2
C. 121 3
D. 121 6
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0