Phương pháp:
+) Lấy tích phân từ 0 đến 2 hai vế của giả thiết.
+) Sử dụng phương pháp đổi biến để biến dổi các tích phân.
Cách giải:
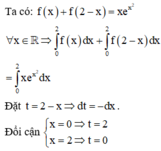
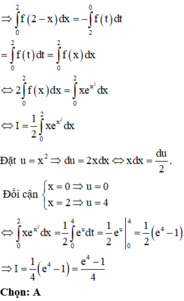
Phương pháp:
+) Lấy tích phân từ 0 đến 2 hai vế của giả thiết.
+) Sử dụng phương pháp đổi biến để biến dổi các tích phân.
Cách giải:
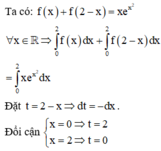
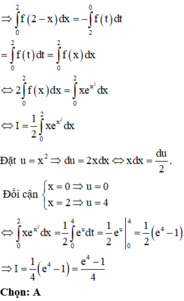
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [ 0 ; 2 ] và thỏa mãn f ( 0 ) = 2 , ∫ 0 2 ( 2 x - 4 ) . f ' ( x ) d x = 4 . Tính tích phân I = ∫ 0 2 f ( x ) d x .
A. I = 2
B. I = - 2
C. I = 6
D. I = - 6
Cho hàm số f(x) có đạo hàm liên tục trên R thảo mãn x . f ' x - x 2 . e x = f x và f(1) = e. Tính tích phân I = ∫ 1 2 f x d x
A. I = e 2 - 2 e
B. I = e
C. I = e 2
D. I = 3 e 2 - 2 e
Cho hàm số y=f(x) xác định và liên tục trên [1;e] thỏa mãn xf ' ( x ) = x [ f ( x ) ] 2 + 3 f ( x ) + 4 x và f(1) = -3. Tính f(e).
A. 5 2 e
B. - 5 2
C. - 5 2 e
D. 5 2
Cho hàm số f(x) có đạo hàm liên tục trên [1;e] thỏa mãn f e = 0 , ∫ 1 e f ' x 2 d x = e - 2 và ∫ 1 e f x x d x = e - 2 . Tích phân ∫ 1 e f x d x bằng:
A. 2e
B. 3 - e 2 4
C. -2e
D. e 2 - 3 4
Cho f(x) là hàm số chẵn, liên tục trên ℝ thỏa mãn ∫ 0 1 f x d x = 2018 và g(x) là hàm số liên tục trên ℝ thỏa mãn g x + g − x = 1 , ∀ x ∈ ℝ . Tính tích phân I = ∫ − 1 1 f x . g x d x
A. I = 2018
B. I = 1009 2
C. I = 4036
D. I = 1008
Cho hàm số f liên tục trên ℝ thỏa mãn f x + f - x = 2 + 2 cos 2 x , với mọi x ϵ ℝ. Giá trị của tích phân I = ∫ - π 2 π 2 là
A. -2
B. -7
C. 7
D. 2
Cho hàm số y=f(x) liên tục và có đạo hàm trên R thỏa mãn f(2)=-2, ∫ 0 2 f x d x = 1. Tính tích phân I = ∫ 0 4 f ' x d x .
A. I = -10
B. I = -5
C. I = 0
D. I = -18
Cho hàm số y = f(x) liên tục và có đạo hàm trên ℝ thỏa mãn f 2 = - 2 ; ∫ 0 2 f x d x = 1 . Tính tích phân I = ∫ 0 4 f ' x d x
A. I = -10
B. I = -5
C. I = 0
D. I = -18
Cho hàm số y=f(x) liên tục trên ℝ và thỏa mãn f(4-x)=f(x) . Biết ∫ 1 3 x f x d x = 5 . Tính I = ∫ 1 3 f x d x
A. I = 5 2
B. I = 7 2
C. I = 9 2
D. I = 11 2
Cho hàm số f(x) liên tục trên ℝ thỏa mãn f x 3 + 1 = 2 x − 1 , ∀ x ∈ ℝ . Tính tích phân I = ∫ 0 2 f x d x .
A. I = -2
B. I = 5 2
C. I = - 4
D. I = 6