Các câu hỏi tương tự
Cho hàm số yf(x) có đạo hàm liên tục trên R. Biết f(1)e và
(
x
+
2
)
f
(
x
)
x
f
(
x
)
-
x
3
, với mọi x thuộc R. Tính f(2). A.
4
e
2
-
4
e
+
4
B.
4...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Biết f(1)=e và ( x + 2 ) f ( x ) = x f ' ( x ) - x 3 , với mọi x thuộc R. Tính f(2).
A. 4 e 2 - 4 e + 4
B. 4 e 2 - 2 e + 1
C. 2 e 3 - 2 e + 2
D. 4 e 2 + 4 e - 4
Cho hàm số f(x) xác định trên R thỏa mãn f (x)
e
x
+
e
-
x
-
2
, f(0)5 và
f
ln
1
4
0
.Giá trị của biểu thức
S
f
-...
Đọc tiếp
Cho hàm số f(x) xác định trên R thỏa mãn f' (x)= e x + e - x - 2 , f(0)=5 và f ln 1 4 = 0 .Giá trị của biểu thức S = f - ln 6 + f ln 4 bằng:
A. S= 31/2.
B. S= 9/2.
C. S= 5/2.
D. S= -7/2
Cho hàm số yf(x) xác định và liên tục trên [0;2] thỏa mãn
e
x
f
2
(
x
)
+
f
(
x
)
f
(
x
)
-...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên [0;2] thỏa mãn e x f 2 ( x ) + f ( x ) = f ' ( x ) - 1 e x và f(0)=1. Tính f(2).
A. 1 e 2
B. - 5 3 e 2
C. - 1 e 2
D. - 2 3 e 2
Cho hàm số f(x) xác định trên
ℝ
thỏa mãn
f
x
e
x
+
e
-
x
-
2
,
f
0
5
và
f
ln
1
4...
Đọc tiếp
Cho hàm số f(x) xác định trên ℝ thỏa mãn f ' x = e x + e - x - 2 , f 0 = 5 và f ln 1 4 = 0 . Giá trị của biểu thức S = f - ln 16 + f ln 4 bằng
A. 31 2 .
B. S = 9 2 .
C. S = 5 2 .
D. S = 11 2
Cho hàm số f(x) có đạo hàm f(x) liên tục trên đoạn [1;e] thỏa mãn
f
1
1
2
và
x
.
f
x
x
f
2
x
-
3
f
x
+
1
x
,
∀
x
∈
1
;...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f'(x) liên tục trên đoạn [1;e] thỏa mãn f 1 = 1 2 và x . f ' x = x f 2 x - 3 f x + 1 x , ∀ x ∈ 1 ; e . Giá trị của f(e) bằng
A. 3 2 e
B. 4 3 e
C. 3 4 e
D. 2 3 e
Cho hàm số f(x) có đạo hàmf(x) xác định và liên tục trên đoạn [0;6]. Đồ thị hàm số yf(x) như hình vẽ bên. Biết f(0)f(3)f(6)-1,f(1)f(5)1. Số điểm cực trị của hàm số
y
[
f
(
x
)
]
2
trên đoạn [0;6] là A. 5. B. 7. C. 9. D. 8.
Đọc tiếp
Cho hàm số f(x) có đạo hàmf'(x) xác định và liên tục trên đoạn [0;6]. Đồ thị hàm số y=f'(x) như hình vẽ bên. Biết f(0)=f(3)=f(6)=-1,f(1)=f(5)=1. Số điểm cực trị của hàm số y = [ f ( x ) ] 2 trên đoạn [0;6] là
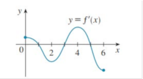
A. 5.
B. 7.
C. 9.
D. 8.
Cho hàm số f(x) có đạo hàm liên tục trên [1;e] thỏa mãn
f
e
0
,
∫
1
e
f
x
2
d
x
e
-
2
và
∫
1
e
f
x...
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên [1;e] thỏa mãn f e = 0 , ∫ 1 e f ' x 2 d x = e - 2 và ∫ 1 e f x x d x = e - 2 . Tích phân ∫ 1 e f x d x bằng:
A. 2e
B. 3 - e 2 4
C. -2e
D. e 2 - 3 4
Cho hàm số yf(x) có đạo hàm liên tục trên (1;+∞) và thỏa mãn
x
f
(
x
)
-
2
f
(
x
)
.
l
n
x
x
3
-
f
(
x
)
,∀x∈(1;+∞); biết
f
(...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên (1;+∞) và thỏa mãn x f ' ( x ) - 2 f ( x ) . l n x = x 3 - f ( x ) ,∀x∈(1;+∞); biết f ( e 3 ) = 3 e . Giá trị f(2) thuộc khoảng nào dưới đây
A. ( 12 ; 25 / 2 )
B. ( 13 ; 27 / 2 )
C. ( 23 / 2 ; 12 )
D. ( 14 ; 29 / 2 )
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f(x) thỏa mãn
f
(
x
)
(
1
-
x
)
(
x
+
2
)
g
(
x
)
+
2018
với
g
(
x
)
0
,
∀
x
∈
R
. Hàm số
y
f
(...
Đọc tiếp
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f'(x) thỏa mãn f ' ( x ) = ( 1 - x ) ( x + 2 ) g ( x ) + 2018 với g ( x ) < 0 , ∀ x ∈ R . Hàm số y = f ( 1 - x ) + 2018 x + 2019 nghịch biến trên khoảng nào dưới đây?
A . ( 1 ; + ∞ ) .
B . ( 0 ; 3 ) .
C . ( - ∞ ; 3 ) .
D . ( 4 ; + ∞ ) .