Các câu hỏi tương tự
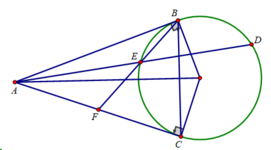
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BCb) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.d) Tính theo R diện tích tam giác BDC.
Đọc tiếp
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC
b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.
c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.
d) Tính theo R diện tích tam giác BDC.
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R. c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC. d) Tính theo R diện tích tam giác BDC.
Đọc tiếp
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R. c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC. d) Tính theo R diện tích tam giác BDC.
Cho (O; R) và một điểm A ở ngoài đường tròn sao cho OA 3R. Từ A vẽ 2 tiếp tuyến AB,AC đến (O) với B và C là các tiếp điểm.a) Chứng minh tứ giác OBAC nội tiếpb) Từ B vẽ đường thẳng song song với AC cắt (O) tại D. Đường thẳng AD cắt đường tròntại E và tia BE cắt AC tại F. Chứng minh rằng F là trung điểm của ACc) Gọi H là giao điểm của BC và OA. Chứng minh rằng HB là tia phân giác của góc EHD.
Đọc tiếp
Cho (O; R) và một điểm A ở ngoài đường tròn sao cho OA = 3R. Từ A vẽ 2 tiếp tuyến AB,
AC đến (O) với B và C là các tiếp điểm.
a) Chứng minh tứ giác OBAC nội tiếp
b) Từ B vẽ đường thẳng song song với AC cắt (O) tại D. Đường thẳng AD cắt đường tròn
tại E và tia BE cắt AC tại F. Chứng minh rằng F là trung điểm của AC
c) Gọi H là giao điểm của BC và OA. Chứng minh rằng HB là tia phân giác của góc EHD.
Cho đường tròn (O;R) và 1 điểm A nằm ngoài (O) sao cho OA3R. Từ điểm A vẽ 2 tiếp tuyến AB,AC tới (O) (B,C là tiếp điểm)a, Chứng minh tứ giác OBAC nội tiếp b, Từ B vẽ đường thẳng song song với AC cắt (O) tại D (D khác B); AD cắt (O) tại E (E khác D). Chứng minh AE.ADAB^2,từ đó tính tích AD.AE theo Rc, Chứng minh CEABECd, Tia BE cắt AC tại F. Chứng minh F là trung điểm của AC
Đọc tiếp
Cho đường tròn (O;R) và 1 điểm A nằm ngoài (O) sao cho OA=3R. Từ điểm A vẽ 2 tiếp tuyến AB,AC tới (O) (B,C là tiếp điểm)
a, Chứng minh tứ giác OBAC nội tiếp
b, Từ B vẽ đường thẳng song song với AC cắt (O) tại D (D khác B); AD cắt (O) tại E (E khác D). Chứng minh AE.AD=AB^2,từ đó tính tích AD.AE theo R
c, Chứng minh CEA=BEC
d, Tia BE cắt AC tại F. Chứng minh F là trung điểm của AC
Từ điếm A ở ngoài đường tròn (O;R) vẽ các tiếp tuyến AB,AC đến (O) với B,C là các tiếp điểma/ Chứng minh OA vuông góc BC tại H và tứ giác OBAC nội tiếp đường trònb/ Từ A vẽ cát tuyến ADE (không qua O) cắt (O) tại D và E (D nằm giữa A và E). Chứng minh: AD.AE AB2c/ Vẽ dây cung BM song song với DE. Gọi giao điểm của CM và DE là i. Chứng minh i trung điểm DEmọi người giúp mik với ạ
Đọc tiếp
Từ điếm A ở ngoài đường tròn (O;R) vẽ các tiếp tuyến AB,AC đến (O) với B,C là các tiếp điểm
a/ Chứng minh OA vuông góc BC tại H và tứ giác OBAC nội tiếp đường tròn
b/ Từ A vẽ cát tuyến ADE (không qua O) cắt (O) tại D và E (D nằm giữa A và E). Chứng minh: AD.AE= AB2
c/ Vẽ dây cung BM song song với DE. Gọi giao điểm của CM và DE là i. Chứng minh i trung điểm DE
mọi người giúp mik với ạ
Cho điểm A nằm ngoài đường tròn (O,R) từ A kẻ hai tiếp tuyến AB,AC và cát tuyến ADE( B,C là hai tiếp điểm ,O nằm trong góc BAE ) BC cắt OA tại I
a/Chứng minh Tứ giác ABOC nội tiếp và OA vuông góc với BC
b/Chứng minh OI.IA =BC^2/4 và AB.AC = AD.AE
c/Vẽ đường kính BK của (O),tia KD cắt OA tại F. Chứng minh FB vuông góc EB
Cho đường trong (O) và điểm A nằm bên ngoài đường tròn (O) sao cho OA=3R. Vẽ các tiếp tuyến AB,AC với đường tròn (O) (B và C là hai tiếp tuyến)
a,Chứng minh tứ giác OBAC nội tiếp
b,Qua B kẻ đường thẳng song song với AC cắt (O) tại D(khác B). Đường thẳng AD cắt (O) tại E. Chứng minh: AB2 = AE.AD
c,Chứng minh tia đối của tia EC là tia phân giác của góc BEA
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.
Cho đường tròn (O ; R) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp tuyến). Gọi H là giao điểm của OA và BC. a) Chứng minh: OA vuông góc BC và OH.OAR² b) Kẻ đường kính BD của (O), AD cắt (O) tại E. Chứng minh: AH.AO AE.AD c) Chứng minh: HC là phân giác của góc DHE
Đọc tiếp
Cho đường tròn (O ; R) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp tuyến). Gọi H là giao điểm của OA và BC. a) Chứng minh: OA vuông góc BC và OH.OA=R² b) Kẻ đường kính BD của (O), AD cắt (O) tại E. Chứng minh: AH.AO= AE.AD c) Chứng minh: HC là phân giác của góc DHE