Các câu hỏi tương tự
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R. c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC. d) Tính theo R diện tích tam giác BDC.
Đọc tiếp
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R. c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC. d) Tính theo R diện tích tam giác BDC.
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BCb) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.d) Tính theo R diện tích tam giác BDC.
Đọc tiếp
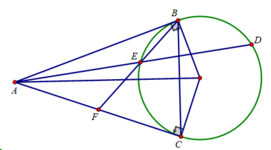
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC
b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.
c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.
d) Tính theo R diện tích tam giác BDC.
Cho điểm A nằm ngoài đường tròn (O;R)sao cho OA2R .Kẻ hai tiếp tuyến AB và AC . B,C là các tiếp điểm. Qua B kẻ dây BE//AC . Cát tuyến AE cắt (O) tại D ( D nằm giữa O và E ) . Gọi F là trung điểm DE
a) chứng minh A,B,F,O,C cùng thuộc 1 đường tròn
b) Tia BD cắt AC tại I . Chứng minh IC² ID.IB,
I là trung điểm AC
c) Tia BT cắt (O) tại K(K≠B). Gọi T là giao điểm giữa OA với O(T nằm giữa O và A) . KT cắt BC tại H. Chứng minh rằng TC là tiếp tuyến của đường tròn ngoại tiếp ∆CHK
Giúp vs cảm ơn
Đọc tiếp
Cho điểm A nằm ngoài đường tròn (O;R)sao cho OA>2R .Kẻ hai tiếp tuyến AB và AC . B,C là các tiếp điểm. Qua B kẻ dây BE//AC . Cát tuyến AE cắt (O) tại D ( D nằm giữa O và E ) . Gọi F là trung điểm DE a) chứng minh A,B,F,O,C cùng thuộc 1 đường tròn b) Tia BD cắt AC tại I . Chứng minh IC² = ID.IB, I là trung điểm AC c) Tia BT cắt (O) tại K(K≠B). Gọi T là giao điểm giữa OA với O(T nằm giữa O và A) . KT cắt BC tại H. Chứng minh rằng TC là tiếp tuyến của đường tròn ngoại tiếp ∆CHK Giúp vs cảm ơn
Cho đường tròn tâm O và điểm A nằm bên ngoài đường tròn, từ A vẽ tiếp tuyến AB với đường tròn (B là tiếp điểm). Kẻ đường kính BC của đường tròn(O). AC cắt đường tròn (O) tại D (D khác C).a) Chứng minh: BD ⊥ AC và AB2 AD.ACb) Từ C vẽ dây CE // OA; BE cắt OA tại H. Chứng minh H là trung điểm của BE và AE là tiếp tuyến của đường tròn (O)c) Chứng minh góc OCH góc OAC.d) Tia OA cắt đường tròn (O) tại F. Chứng minh FA.CH HF.CA
Đọc tiếp
Cho đường tròn tâm O và điểm A nằm bên ngoài đường tròn, từ A vẽ tiếp tuyến AB với đường tròn (B là tiếp điểm). Kẻ đường kính BC của đường tròn(O). AC cắt đường tròn (O) tại D (D khác C).
a) Chứng minh: BD ⊥ AC và AB2 = AD.AC
b) Từ C vẽ dây CE // OA; BE cắt OA tại H. Chứng minh H là trung điểm của BE và AE là tiếp tuyến của đường tròn (O)
c) Chứng minh góc OCH = góc OAC.
d) Tia OA cắt đường tròn (O) tại F. Chứng minh FA.CH = HF.CA
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.
cho đường tròn (O) từ A ở ngoài đường tròn vẽ hai tiếp tuyến AB và AC(B,C) là các tiếp điểm. OA cắt BC tại E. Gọi I là trung điểm BE, đường thẳng đi qua I và vuông góc OI cắt các tia AB,AC theo thứ tự tại D và F.chứng minh F là trung điểm BC
Lấy Điểm A nằm ngoài đường tròn ( O;R) sao cho AO = 3R. Vẽ hai tiếp tuyến AB; AC với đường tròn ( B;C là tiếp điểm). a) Chứng minh: Tứ giác ABOC nội tiếp đường tròn. b) Qua A vẽ cát tuyến AEF với (O) sao cho E nằm giữa A và F và cắt đoạn thẳng OB tại K. Chứng minh: AC^2 = AE.AF c) Từ E vẽ đường thẳng vuông góc với OB cắt BC tại M, I là trung điểm của EF. Chứng minh: MI // FB.
Bài 1: Cho (O;R) và điểm A nằm ngoài (O) sao cho OA3R. Từ A vẽ 2 tiếp tuyến AB; AC với (O)a) CMR: Tứ giác OBAC nội tiếpb) CMR: OA ⊥ BCc) Từ B vẽ đường thẳng // AC cắt (O) tại D; AD cắt (O) tại E. Tính AD.AE theo Rd) Tia BE cắt AC tại F. CMR: F là trung điểm ACBài 2: Cho ΔABC nhọn nội tiếp (O); hai điểm B;C cố định. Điểm A di chuyển trên cung lớn BC. Gọi H là hình chiếu của A xuống BC. Gọi M;N lần lượt là hình chiếu của B;C đến đường kính ADa) C/m các điểm A;B;H;M cùng thuộc một đường trònb) C/m...
Đọc tiếp
Bài 1: Cho (O;R) và điểm A nằm ngoài (O) sao cho OA=3R. Từ A vẽ 2 tiếp tuyến AB; AC với (O)
a) CMR: Tứ giác OBAC nội tiếp
b) CMR: OA ⊥ BC
c) Từ B vẽ đường thẳng // AC cắt (O) tại D; AD cắt (O) tại E. Tính AD.AE theo R
d) Tia BE cắt AC tại F. CMR: F là trung điểm AC
Bài 2: Cho ΔABC nhọn nội tiếp (O); hai điểm B;C cố định. Điểm A di chuyển trên cung lớn BC. Gọi H là hình chiếu của A xuống BC. Gọi M;N lần lượt là hình chiếu của B;C đến đường kính AD
a) C/m các điểm A;B;H;M cùng thuộc một đường tròn
b) C/m ΔHMN ∽ ΔABC
c) Gọi I;E lần lượt là trung điểm BC và AB. C/m IE là trung trực của HM