Các câu hỏi tương tự
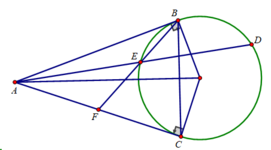
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R. c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC. d) Tính theo R diện tích tam giác BDC.
Đọc tiếp
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R. c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC. d) Tính theo R diện tích tam giác BDC.
Cho đường tròn (O;R) và 1 điểm A nằm ngoài (O) sao cho OA3R. Từ điểm A vẽ 2 tiếp tuyến AB,AC tới (O) (B,C là tiếp điểm)a, Chứng minh tứ giác OBAC nội tiếp b, Từ B vẽ đường thẳng song song với AC cắt (O) tại D (D khác B); AD cắt (O) tại E (E khác D). Chứng minh AE.ADAB^2,từ đó tính tích AD.AE theo Rc, Chứng minh CEABECd, Tia BE cắt AC tại F. Chứng minh F là trung điểm của AC
Đọc tiếp
Cho đường tròn (O;R) và 1 điểm A nằm ngoài (O) sao cho OA=3R. Từ điểm A vẽ 2 tiếp tuyến AB,AC tới (O) (B,C là tiếp điểm)
a, Chứng minh tứ giác OBAC nội tiếp
b, Từ B vẽ đường thẳng song song với AC cắt (O) tại D (D khác B); AD cắt (O) tại E (E khác D). Chứng minh AE.AD=AB^2,từ đó tính tích AD.AE theo R
c, Chứng minh CEA=BEC
d, Tia BE cắt AC tại F. Chứng minh F là trung điểm của AC
Cho (O; R) và một điểm A ở ngoài đường tròn sao cho OA 3R. Từ A vẽ 2 tiếp tuyến AB,AC đến (O) với B và C là các tiếp điểm.a) Chứng minh tứ giác OBAC nội tiếpb) Từ B vẽ đường thẳng song song với AC cắt (O) tại D. Đường thẳng AD cắt đường tròntại E và tia BE cắt AC tại F. Chứng minh rằng F là trung điểm của ACc) Gọi H là giao điểm của BC và OA. Chứng minh rằng HB là tia phân giác của góc EHD.
Đọc tiếp
Cho (O; R) và một điểm A ở ngoài đường tròn sao cho OA = 3R. Từ A vẽ 2 tiếp tuyến AB,
AC đến (O) với B và C là các tiếp điểm.
a) Chứng minh tứ giác OBAC nội tiếp
b) Từ B vẽ đường thẳng song song với AC cắt (O) tại D. Đường thẳng AD cắt đường tròn
tại E và tia BE cắt AC tại F. Chứng minh rằng F là trung điểm của AC
c) Gọi H là giao điểm của BC và OA. Chứng minh rằng HB là tia phân giác của góc EHD.
Cho O R; và điểm A nằm ngoài đường tròn với OA R 2 . Từ A vẽ hai tiếp tuyến AB AC , của đường tròn O (B C, là tiếp điểm). Vẽ dây BE của đường tròn O song song với AC ; AE cắt O tại D khác E ; BD cắt AC tại S . Gọi M là trung điểm của đoạn DE . a) Chứng minh năm điểm A B C O M , , , , cùng thuộc một đường tròn. Xác định tâm và bán kính của đường tròn này. b) Chứng minh 2 SC SB SD . . c) Hai đường thẳng DE và BC cắt nhau tại Q ; đường thẳng SQ cắt BE tại H . Chứng minh ba điểm H O C ,...
Đọc tiếp
Cho O R; và điểm A nằm ngoài đường tròn với OA R 2 . Từ A vẽ hai tiếp tuyến AB AC , của đường tròn O (B C, là tiếp điểm). Vẽ dây BE của đường tròn O song song với AC ; AE cắt O tại D khác E ; BD cắt AC tại S . Gọi M là trung điểm của đoạn DE . a) Chứng minh năm điểm A B C O M , , , , cùng thuộc một đường tròn. Xác định tâm và bán kính của đường tròn này. b) Chứng minh 2 SC SB SD . . c) Hai đường thẳng DE và BC cắt nhau tại Q ; đường thẳng SQ cắt BE tại H . Chứng minh ba điểm H O C , , thẳng hàng.
Cho (O;R) và điểm A nằm ngoài đường tròn với OA > 2R. Từ A và B vẽ 2 tiếp tuyến AB, AC của đường tròn O (B,C là các tiếp điểm). VẼ dây BE của đường tròn O song song với AC; AE cắt (O) tại D khác E; BD cắt AC tại S. Gọi M là trung điểm của DE. Hai đường thẳng DE và BC cắt nhau tại V; đường thẳng SV cắt BE tại H. Chứng minh 3 điểm H,O,C thẳng hàng.
Cho (O; R) và 1 điểm A ở ngoài đường tròn sao cho OA = 3R. Từ A vẽ 2 tiếp tuyên AB, AC đến đường tròn. Từ B vẽ đường thẳng song song với AC cắt (O) tại D. Đường thẳng AD cắt (O) tại E. Chứng minh AB^2 = AE . AD. Chứng minh BC . CE = AC . BE
Câu 4:( 4 điểm ) Từ điểm M nằm ngoài đường tròn ( O,R ) sao cho OM 3R, vẽ các tiếp tuyến MA, MB với đường tròn ( O,R ) (A, B là các tiếp điểm). a ) Chứng minh: Tứ giác MAOB nội tiếp và OM là đường trung trực của đoạn AB. b ) Tính độ dài đoạn thẳng MA, AB theo R. c) Vẽ dây AC song song MB, đường thẳng MC cắt đường tròn (O,R) tại điểm thứ hai là D, tia AD cắt MB tại E. Chứng minh: E là trung điểm của đoạn MB
Đọc tiếp
Câu 4:( 4 điểm ) Từ điểm M nằm ngoài đường tròn ( O,R ) sao cho OM = 3R, vẽ các tiếp tuyến MA, MB với đường tròn ( O,R ) (A, B là các tiếp điểm). a ) Chứng minh: Tứ giác MAOB nội tiếp và OM là đường trung trực của đoạn AB. b ) Tính độ dài đoạn thẳng MA, AB theo R. c) Vẽ dây AC song song MB, đường thẳng MC cắt đường tròn (O,R) tại điểm thứ hai là D, tia AD cắt MB tại E. Chứng minh: E là trung điểm của đoạn MB
Cho đường tròn (O;R). Từ điểm A ngoài đường tròn kẻ các tiếp tuyến AB,AC với đường tròn (B,C là tiếp điểm). Gọi H là giao điểm của AO và BC
a) Cm: AO vuông góc với BC tại H
b) Vẽ đường kính BD của (O), cm: DC song song AO
c) AD cắt (O) tại E (E khác D). CM AE.AD=AH.AO
d) Qua vẽ đường thẳng vuông góc với AB. Đường thẳng này cắt OC tại F. CM: OA^2 = 2OC.OF
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BCb) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.d) Tính theo R diện tích tam giác BDC.
Đọc tiếp
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC
b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.
c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.
d) Tính theo R diện tích tam giác BDC.