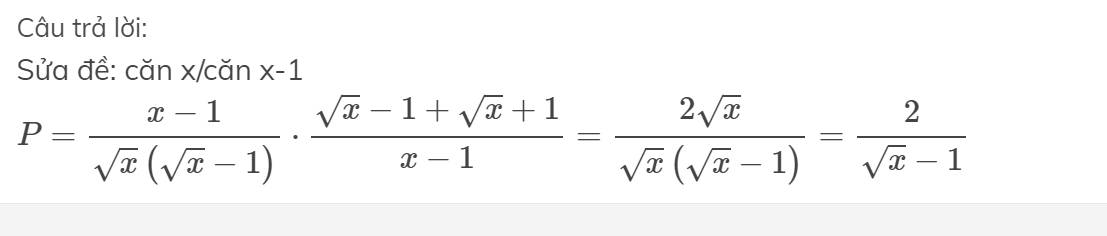Các câu hỏi tương tự
Cho biểu thức P= \(\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\left(1-\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\)
Rút gọn biểu thức trên
5 tháng 9 2023 lúc 10:53
RÚT GỌN BIỂU THỨC:
20) \(E = \left(\dfrac{x\sqrt{x} - 1}{x - \sqrt{x}} - \dfrac{x\sqrt{x} +1}{x + \sqrt{x}}\right) + \left(\sqrt{x} - \dfrac{1}{\sqrt{x}}\right)\left(\dfrac{\sqrt{x} + 1}{\sqrt{x} - 1} + \dfrac{\sqrt{x} - 1}{\sqrt{x} + 1}\right)\)
5 tháng 9 2023 lúc 19:47
RÚT GỌN CÁC BIỂU THỨC SAU:21) A left(dfrac{xsqrt{x} + 1}{x - 1} - dfrac{x - 1}{sqrt{x} - 1}right) : left(sqrt{x} + dfrac{sqrt{x}}{sqrt{x} - 1}right) 22) A left(dfrac{x}{sqrt{x} - 1} - sqrt{x}right) : left(dfrac{sqrt{x} + 1}{sqrt{x}} - dfrac{1}{1 - sqrt{x}} + dfrac{2 - x}{x - sqrt{x}}right)23) A left(dfrac{sqrt{x} - 4}{x - 2sqrt{x}} - dfrac{3}{2 - sqrt{x}}right) : left(dfrac{sqrt{x} + 2}{sqrt{x}} - dfrac{sqrt{x}}{sqrt{x} - 2}right)24) A left(dfrac{2x + 1}{xsqrt{x} - 1} + dfrac{1}{1 - sqrt{x}}...
Đọc tiếp
RÚT GỌN CÁC BIỂU THỨC SAU:
21) \(A = \left(\dfrac{x\sqrt{x} + 1}{x - 1} - \dfrac{x - 1}{\sqrt{x} - 1}\right) : \left(\sqrt{x} + \dfrac{\sqrt{x}}{\sqrt{x} - 1}\right) \)
22) \(A = \left(\dfrac{x}{\sqrt{x} - 1} - \sqrt{x}\right) : \left(\dfrac{\sqrt{x} + 1}{\sqrt{x}} - \dfrac{1}{1 - \sqrt{x}} + \dfrac{2 - x}{x - \sqrt{x}}\right)\)
23) \(A = \left(\dfrac{\sqrt{x} - 4}{x - 2\sqrt{x}} - \dfrac{3}{2 - \sqrt{x}}\right) : \left(\dfrac{\sqrt{x} + 2}{\sqrt{x}} - \dfrac{\sqrt{x}}{\sqrt{x} - 2}\right)\)
24) \(A = \left(\dfrac{2x + 1}{x\sqrt{x} - 1} + \dfrac{1}{1 - \sqrt{x}}\right) : \left(1 - \dfrac{x - 2}{x + \sqrt{x} + 1}\right)\)
25) \(A = 1 : \left(\dfrac{x + 2\sqrt{x} - 2}{x\sqrt{x} + 1} - \dfrac{\sqrt{x} -1}{x - \sqrt{x} + 1} + \dfrac{1}{\sqrt{x} + 1}\right)\)
26) \(A = \left(\dfrac{\sqrt{x}}{\sqrt{x} + 2} - \dfrac{3}{2 - \sqrt{x}} + \dfrac{3\sqrt{x} - 2}{x - 2}\right) : \left(\dfrac{\sqrt{x} + 3}{\sqrt{x} - 2} + \dfrac{2\sqrt{x}}{2\sqrt{x} - x}\right)\)
27) \(P = \left(\dfrac{4\sqrt{x}}{2 + \sqrt{x}} + \dfrac{8}{4 - x}\right) : \left(\dfrac{\sqrt{x} - 1}{x - 2\sqrt{x}} - \dfrac{2}{\sqrt{x}}\right)\)
Cho biểu thức
P= \(\left(\dfrac{\sqrt{x-1}}{3+\sqrt{x-1}}+\dfrac{x+8}{\left(3-\sqrt{x-1}\right)\left(3+\sqrt{x-1}\right)}\right):\left(\dfrac{3\sqrt{x-1}+1}{x-1-3\sqrt{x-1}}-\dfrac{1}{\sqrt{x-1}}\right)\)
a) Rút gọn P .
b) Tính giá trị của biểu thức P khi x= \(\sqrt{3+2\sqrt{2}}-\left(\sqrt{5}+1\right)\sqrt{3-2\sqrt{2}}+\sqrt{5}\left|1-\sqrt{2}\right|\)
\(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}+\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)\times\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\right)\)
rút gọn biểu thức
5 tháng 9 2023 lúc 10:34
RÚT GỌN BIỂU THỨC:
19) \(A = \left(\dfrac{1}{\sqrt{x}} - \dfrac{1}{\sqrt{x} - 1}\right) : \left(\dfrac{\sqrt{x} + 2}{\sqrt{x} - 1} - \dfrac{\sqrt{x} + 1}{\sqrt{x} - 2}\right)\)
4 tháng 9 2023 lúc 14:30
RÚT GỌN BIỂU THỨC:
12) \(A = \left(\dfrac{x}{\sqrt{x} - 1} - \sqrt{x}\right) : \left(\dfrac{\sqrt{x} + 1}{\sqrt{x}} - \dfrac{1}{1 - \sqrt{x}} + \dfrac{2 - x}{x - \sqrt{x}}\right)\)
4 tháng 9 2023 lúc 10:33
RÚT GỌN BIỂU THỨC:
9) \(A = \left(\dfrac{1}{1 - \sqrt{x}}+\dfrac{1}{1 + \sqrt{x}}\right) : \left(\dfrac{1}{1 - \sqrt{x}}-\dfrac{1}{1 + \sqrt{x}}\right) + \dfrac{1}{1 - \sqrt{x}} \)
Rút gọn biểu thức
\(P=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\right)\)
Mong mn giải cụ thể cho mình với ạ
Cho biểu thức P = \(\dfrac{3\left(x+2\sqrt{x}\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\) ( với x ≥ 0; x ≠ 1 )
a,Rút gọn biểu thức P
b,Tính giá trị của P khi x = \(6-2\sqrt{5}\)