Các câu hỏi tương tự
Cho 3 hàm số
y
f
x
,
y
f
f
x
,
y
f
x
2
+
4
có đồ thị lần lượt là
C
1
,
C
2...
Đọc tiếp
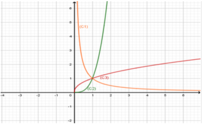
Cho 3 hàm số y = f x , y = f f x , y = f x 2 + 4 có đồ thị lần lượt là C 1 , C 2 , C 3 . Đường thẳng x = 1 cắt C 1 , C 2 , C 3 lần lượt tại các điểm M, N, P. Biết rằng phương trình tiếp tuyến của C 1 tại M, của C 2 tại N và của C 3 tại P lần lượt là y = 3 x + 2 , y = 12 x - 5 v à y = a x + b . Tổng a + b bằng
A. 8
B. 7
C. 9
D. -1
Cho hàm số yf(x); yf(f(x));
y
f
x
2
+
4
có đồ thị lần lượt là
C
1
,
C
2
,
C
3
. Đường thẳng x1 cắt
C
1
,
C...
Đọc tiếp
Cho hàm số y=f(x); y=f(f(x)); y = f x 2 + 4 có đồ thị lần lượt là C 1 , C 2 , C 3 . Đường thẳng x=1 cắt C 1 , C 2 , C 3 lần lượt tại M,N,P. Biết phương trình tiếp tuyến của C 1 tại M và của C 2 tại N lần lượt là y=3x+2 vày=12x-5. Biết phương trình tiếp tuyến của C 3 tại P có dạng y=ax+b Tìm a+b
A. 7.
B. 9.
C. 8.
D. 6.
Cho các hàm số
y
f
x
,
y
f
f
x
,
y
f
x
2
+
4
có đồ thị lần lượt là
C
1
;
C
2
;...
Đọc tiếp
Cho các hàm số y = f x , y = f f x , y = f x 2 + 4 có đồ thị lần lượt là C 1 ; C 2 ; C 3 . Đường thẳng x=1 cắt C 1 ; C 2 ; C 3 lần lượt tại M, N, P. Biết phương trình tiếp tuyến của C 1 tại M và của C 2 tại N lần lượt là y=3x+2 và y=12x-5. Phương trình tiếp tuyến của C 3 tại P bằng:
A. y=8x-1
B. y=4x+3
C. y=2x+5
D. y=3x+4
Cho các hàm số
y
f
x
;
y
f
f
x
;
y
f
x
2
+
4
có đồ thị lần lượt là
C
1
;
C
2
;...
Đọc tiếp
Cho các hàm số y = f x ; y = f f x ; y = f x 2 + 4 có đồ thị lần lượt là C 1 ; C 2 ; C 3 . Đường thẳng x = 1 cắt C 1 ; C 2 ; C 3 lần lượt tại M, N, P. Biết rằng phương trình tiếp tuyến của C 1 tại M và của C 2 tại N lần lượt là
A. y = 8 x − 1
B. y = 4 x + 3
C. y = 2 x + 5
D. y = 3 x + 4
Cho hàm số yf(x) có đạo hàm cấp một f (x) và đạo hàm cấp hai trên
ℝ
. Biết đồ thị của hàm số
y
f
x
,
y
f
x
v
à
y
f
x
là một trong các đường cong
C
1
,
C
2...
Đọc tiếp
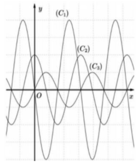
Cho hàm số y=f(x) có đạo hàm cấp một f '(x) và đạo hàm cấp hai trên ℝ . Biết đồ thị của hàm số y = f x , y = f ' x v à y = f " x là một trong các đường cong C 1 , C 2 , C 3 ở hình vẽ bên. Hỏi đồ thị của hàm số y = f x , y = f ' x v à y = f " x lần lượt theo thứ tự nào dưới đây ?
A. C 2 , C 1 , C 3
B. C 1 , C 2 , C 3
C. C 3 , C 2 , C 1
D. C 3 , C 1 , C 2
Trong không gian (Oxyz), cho mặt cầu
(
S
)
:
(
x
-
1
)
2
+
(
y
-
1
)
2
+
(
z
+
2
)
2
4
và điểm...
Đọc tiếp
Trong không gian (Oxyz), cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 4 và điểm A(1;1;-1). Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu (S) theo ba giao tuyến là các đường tròn ( C 1 ) , ( C 2 ) , ( C 3 ) . Tổng bán kính của ba đường tròn ( C 1 ) , ( C 2 ) , ( C 3 ) là
A. 2 + 2 3
B. 3 3
C. 4 + 3
D. 6
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):
(
x
-
1
)
2
+
(
y
-
1
)
2
+
(
z
+
2
)
2
4
và điểm A(1;1;-1). Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu (S) theo ba giao tuyến là các đường tròn
(
C...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 4 và điểm A(1;1;-1). Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu (S) theo ba giao tuyến là các đường tròn ( C 1 ) , ( C 2 ) , ( C 3 ) . Tính tổng diện tích của ba đường tròn ( C 1 ) , ( C 2 ) , ( C 3 )
A. 4 π
B. 12 π
C. 11 π
D. 3 π
Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường tròn
C
1
và
C
2
lần lượt có phương trình
x
-
1
2
+
y
-
2
2
1
v
à
...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường tròn C 1 và C 2 lần lượt có phương trình x - 1 2 + y - 2 2 = 1 v à x + 1 2 + y 2 = 1 . Biết đồ thị hàm số y = a x + b x + c đi qua tâm của C 1 , đi qua tâm của C 2 và có các đường tiệm cận tiếp xúc với cả C 1 và C 2 . Tổng a + b + c là
A. 8.
B. 2.
C. -1.
D. 5.
Cho bốn đường cong được kí hiệu là (C1), C2), (C3) và (C4) như hình vẽ bên. Hàm số
y
log
1
3
x
có đồ thị là đường cong A. (C3) B. (C4). C. (C2) D. (C1).
Đọc tiếp
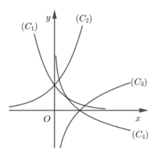
Cho bốn đường cong được kí hiệu là (C1), C2), (C3) và (C4) như hình vẽ bên. Hàm số y = log 1 3 x có đồ thị là đường cong
A. (C3)
B. (C4).
C. (C2)
D. (C1).
Cho bốn hàm số
y
3
x
1
,
y
1
3
x
2
,
y
4
x
3
,
y
1
4
x...
Đọc tiếp
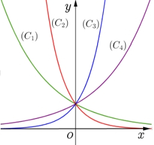
Cho bốn hàm số y = 3 x 1 , y = 1 3 x 2 , y = 4 x 3 , y = 1 4 x 4 có đồ thị là 4 đường cong theo phía trên đồ thị, thứ tự từ trái qua phải là C 1 , C 2 , C 3 , C 4 như hình vẽ. Tương ứng hàm số - đồ thị đúng là
A. 1 - C 2 , 2 - C 3 , 3 - C 4 , 4 - C 1
B. 1 - C 1 , 2 - C 2 , 3 - C 3 , 4 - C 4
C. 1 - C 4 , 2 - C 1 , 3 - C 3 , 4 - C 2
D. 1 - C 4 , 2 - C 2 , 3 - C 3 , 4 - C 1