Các câu hỏi tương tự
Cho hàm số yf(x); yf(f(x));
y
f
x
2
+
4
có đồ thị lần lượt là
C
1
,
C
2
,
C
3
. Đường thẳng x1 cắt
C
1
,
C...
Đọc tiếp
Cho hàm số y=f(x); y=f(f(x)); y = f x 2 + 4 có đồ thị lần lượt là C 1 , C 2 , C 3 . Đường thẳng x=1 cắt C 1 , C 2 , C 3 lần lượt tại M,N,P. Biết phương trình tiếp tuyến của C 1 tại M và của C 2 tại N lần lượt là y=3x+2 vày=12x-5. Biết phương trình tiếp tuyến của C 3 tại P có dạng y=ax+b Tìm a+b
A. 7.
B. 9.
C. 8.
D. 6.
Cho các hàm số
y
f
x
,
y
f
f
x
,
y
f
x
2
+
4
có đồ thị lần lượt là
C
1
;
C
2
;...
Đọc tiếp
Cho các hàm số y = f x , y = f f x , y = f x 2 + 4 có đồ thị lần lượt là C 1 ; C 2 ; C 3 . Đường thẳng x=1 cắt C 1 ; C 2 ; C 3 lần lượt tại M, N, P. Biết phương trình tiếp tuyến của C 1 tại M và của C 2 tại N lần lượt là y=3x+2 và y=12x-5. Phương trình tiếp tuyến của C 3 tại P bằng:
A. y=8x-1
B. y=4x+3
C. y=2x+5
D. y=3x+4
Cho hàm số y f(x) có đạo hàm trên R và đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm (2;m) có phương trình là
y
4
x
-
6
. Tiếp tuyến của các đồ thị hàm số
y
f
f
x
và
y
f
3
x
2
-
10...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên R và đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm (2;m) có phương trình là y = 4 x - 6 . Tiếp tuyến của các đồ thị hàm số y = f f x và y = f 3 x 2 - 10 tại điểm có hoành độ bằng 2 có phương trình lần lượt là y = a x + b v à y = c x + d . Tính giá trị của biểu thức S = 4 a + 3 c - 2 b + d
A. S = -26
B. S = 176
C. S = 178
D. S = 174
Cho 3 hàm số
y
f
x
,
y
f
f
x
,
y
f
x
2
+
4
có đồ thị lần lượt là
C
1
,
C
2...
Đọc tiếp
Cho 3 hàm số y = f x , y = f f x , y = f x 2 + 4 có đồ thị lần lượt là C 1 , C 2 , C 3 . Đường thẳng x = 1 cắt C 1 , C 2 , C 3 lần lượt tại các điểm M, N, P. Biết rằng phương trình tiếp tuyến của C 1 tại M, của C 2 tại N và của C 3 tại P lần lượt là y = 3 x + 2 , y = 12 x - 5 v à y = a x + b . Tổng a + b bằng
A. 8
B. 7
C. 9
D. -1
Giả sử đường thẳng yx+m cắt đồ thị (C) của hàm số
y
x
−
1
1
−
2
x
tại hai điểm phân biệt E và F. Gọi
k
1
,
k
2
lần lượt là hệ số góc của các tiếp tuyến với (C) tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức
S...
Đọc tiếp
Giả sử đường thẳng y=x+m cắt đồ thị (C) của hàm số y = x − 1 1 − 2 x tại hai điểm phân biệt E và F. Gọi k 1 , k 2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức S = k 1 4 + k 2 4 − 3 k 1 k 2 .
A. min S = − 1
B. min S = − 5 8
C. min S = 135
D. min S = − 25 81
Giả sử đường thẳng
y
x
+
m
cắt đồ thị (C) của hàm số
y
x
−
1
1
−
2
x
tại hai điểm phân biệt E và F. Gọi
k
1
,
k
2
lần lượt là hệ số góc của các tiếp tuyến với
C
tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức
S...
Đọc tiếp
Giả sử đường thẳng y = x + m cắt đồ thị (C) của hàm số y = x − 1 1 − 2 x tại hai điểm phân biệt E và F. Gọi k 1 , k 2 lần lượt là hệ số góc của các tiếp tuyến với C tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức S = k 1 4 + k 2 4 − 3 k 1 k 2 .
A. min S = − 1
B. min S = − 5 8
C. min S = 135
D. min S = − 25 81
Cho hàm số yf(x) có đồ thị là (C), hàm số yf(x) có đồ thị như hình vẽ bên. Tiếp tuyến với (C) tại điểm có hoành độ x2 cắt (C) tại hai điểm phân biệt có hoành độ lần lượt là a,bGiá trị
(
a
-
b
)
2
thuộc khoảng nào dưới đây A.
(
0
;
9
)
B.
(
12
;
16
)
C.
(
16...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị là (C), hàm số y=f'(x) có đồ thị như hình vẽ bên. Tiếp tuyến với (C) tại điểm có hoành độ x=2 cắt (C) tại hai điểm phân biệt có hoành độ lần lượt là a,b
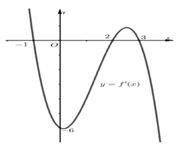
Giá trị ( a - b ) 2 thuộc khoảng nào dưới đây
A. ( 0 ; 9 )
B. ( 12 ; 16 )
C. ( 16 ; + ∞ )
D. ( 9 ; 12 )
Cho hai hàm số đa thức bậc bốn y f(x) và y g(x) có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số y f(x). Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là -3 và cắt nhau tại hai điểm nữa có hoành độ lần lượt là -1 và 3. Tìm tập hợp tất cả các giá trị thực của tham số m để bất phương trình
f
x
≥
g
x
+
m
nghiệm đúng với mọi
x
∈...
Đọc tiếp
Cho hai hàm số đa thức bậc bốn y = f(x) và y = g(x) có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số y = f(x). Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là -3 và cắt nhau tại hai điểm nữa có hoành độ lần lượt là -1 và 3. Tìm tập hợp tất cả các giá trị thực của tham số m để bất phương trình f x ≥ g x + m nghiệm đúng với mọi x ∈ - 3 ; 3 .
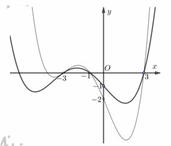
A. - ∞ ; 12 - 8 3 9 .
B. 12 - 10 3 9 ; + ∞ .
C. - ∞ ; 12 - 10 3 9 .
D. 12 - 8 3 9 ; + ∞ .
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là
A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0