Hàm số y = log 1 2 x là hàm nghịch biến và đồ thị của nó đi qua điểm toạ độ (1;0).
Chọn đáp án B.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho bốn hàm số
y
3
x
1
,
y
1
3
x
2
,
y
4
x
3
,
y
1
4
x...
Đọc tiếp
Cho bốn hàm số y = 3 x 1 , y = 1 3 x 2 , y = 4 x 3 , y = 1 4 x 4 có đồ thị là 4 đường cong theo phía trên đồ thị, thứ tự từ trái qua phải là C 1 , C 2 , C 3 , C 4 như hình vẽ. Tương ứng hàm số - đồ thị đúng là
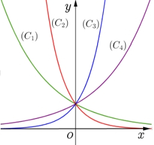
A. 1 - C 2 , 2 - C 3 , 3 - C 4 , 4 - C 1
B. 1 - C 1 , 2 - C 2 , 3 - C 3 , 4 - C 4
C. 1 - C 4 , 2 - C 1 , 3 - C 3 , 4 - C 2
D. 1 - C 4 , 2 - C 2 , 3 - C 3 , 4 - C 1
Cho hàm số yf(x) có đạo hàm cấp một f (x) và đạo hàm cấp hai trên
ℝ
. Biết đồ thị của hàm số
y
f
x
,
y
f
x
v
à
y
f
x
là một trong các đường cong
C
1
,
C
2...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm cấp một f '(x) và đạo hàm cấp hai trên ℝ . Biết đồ thị của hàm số y = f x , y = f ' x v à y = f " x là một trong các đường cong C 1 , C 2 , C 3 ở hình vẽ bên. Hỏi đồ thị của hàm số y = f x , y = f ' x v à y = f " x lần lượt theo thứ tự nào dưới đây ?
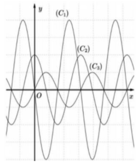
A. C 2 , C 1 , C 3
B. C 1 , C 2 , C 3
C. C 3 , C 2 , C 1
D. C 3 , C 1 , C 2
Cho 3 hàm số
y
f
x
,
y
f
f
x
,
y
f
x
2
+
4
có đồ thị lần lượt là
C
1
,
C
2...
Đọc tiếp
Cho 3 hàm số y = f x , y = f f x , y = f x 2 + 4 có đồ thị lần lượt là C 1 , C 2 , C 3 . Đường thẳng x = 1 cắt C 1 , C 2 , C 3 lần lượt tại các điểm M, N, P. Biết rằng phương trình tiếp tuyến của C 1 tại M, của C 2 tại N và của C 3 tại P lần lượt là y = 3 x + 2 , y = 12 x - 5 v à y = a x + b . Tổng a + b bằng
A. 8
B. 7
C. 9
D. -1
Cho các hàm số
y
f
x
;
y
f
f
x
;
y
f
x
2
+
4
có đồ thị lần lượt là
C
1
;
C
2
;...
Đọc tiếp
Cho các hàm số y = f x ; y = f f x ; y = f x 2 + 4 có đồ thị lần lượt là C 1 ; C 2 ; C 3 . Đường thẳng x = 1 cắt C 1 ; C 2 ; C 3 lần lượt tại M, N, P. Biết rằng phương trình tiếp tuyến của C 1 tại M và của C 2 tại N lần lượt là
A. y = 8 x − 1
B. y = 4 x + 3
C. y = 2 x + 5
D. y = 3 x + 4
Cho các hàm số
y
f
x
,
y
f
f
x
,
y
f
x
2
+
4
có đồ thị lần lượt là
C
1
;
C
2
;...
Đọc tiếp
Cho các hàm số y = f x , y = f f x , y = f x 2 + 4 có đồ thị lần lượt là C 1 ; C 2 ; C 3 . Đường thẳng x=1 cắt C 1 ; C 2 ; C 3 lần lượt tại M, N, P. Biết phương trình tiếp tuyến của C 1 tại M và của C 2 tại N lần lượt là y=3x+2 và y=12x-5. Phương trình tiếp tuyến của C 3 tại P bằng:
A. y=8x-1
B. y=4x+3
C. y=2x+5
D. y=3x+4
Cho hàm số yf(x); yf(f(x));
y
f
x
2
+
4
có đồ thị lần lượt là
C
1
,
C
2
,
C
3
. Đường thẳng x1 cắt
C
1
,
C...
Đọc tiếp
Cho hàm số y=f(x); y=f(f(x)); y = f x 2 + 4 có đồ thị lần lượt là C 1 , C 2 , C 3 . Đường thẳng x=1 cắt C 1 , C 2 , C 3 lần lượt tại M,N,P. Biết phương trình tiếp tuyến của C 1 tại M và của C 2 tại N lần lượt là y=3x+2 vày=12x-5. Biết phương trình tiếp tuyến của C 3 tại P có dạng y=ax+b Tìm a+b
A. 7.
B. 9.
C. 8.
D. 6.
Cho đồ thị hàm số
y
2
x
là đồ thị (
C
1
) như hình vẽ, (
C
2
) là đồ thị đối xứng của (
C
1
) qua trục Oy. Một đường thẳng d song song với Oy cắt đồ thị (
C
1
), (
C
2
) tại 2 điểm A, B như hình vẽ có tung độ lần lượt là a,...
Đọc tiếp
Cho đồ thị hàm số y = 2 x là đồ thị ( C 1 ) như hình vẽ, ( C 2 ) là đồ thị đối xứng của ( C 1 ) qua trục Oy. Một đường thẳng d song song với Oy cắt đồ thị ( C 1 ), ( C 2 ) tại 2 điểm A, B như hình vẽ có tung độ lần lượt là a, b. Giá trị nhỏ nhất của biểu thức P = 4 a 3 + b 3 - 3 a + b 2 a + 2 b - 3 là
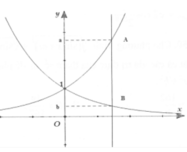
A. 14
B. 0
C. 4
D. - 2
Trong mặt phẳng Oxy cho đường tròn
C
:
x
2
+
y
−
1
2
3
. Hỏi trong bốn đường tròn
C
1
:
x
+
1
2
+...
Đọc tiếp
Trong mặt phẳng Oxy cho đường tròn C : x 2 + y − 1 2 = 3 . Hỏi trong bốn đường tròn C 1 : x + 1 2 + y − 3 2 = 4 , C 2 : x − 1 2 + y 2 = 2 , C 3 : x − 1 2 + y + 3 2 = 3 , C 4 : x 2 + y + 1 2 = 9 đường tròn nào là ảnh của (C) qua phép tịnh tiến.
A. C 1
B. C 2
C. C 3
D. C 4
Cho các đường cong
C
1
:
y
x
3
-
3
x
2
+
4
,
C
2
:...
Đọc tiếp
Cho các đường cong C 1 : y = x 3 - 3 x 2 + 4 , C 2 : y = - x 4 + x 2 - 3 và C 3 : y = 5 x + 2 x - 1 . Hỏi các đường cong nào có tâm đối xứng?
A. C 1 , C 2 v à C 3
B. C 1 v à C 3
C. C 2 v à C 3
D. C 1 v à C 2