Các câu hỏi tương tự
Cho tam giác ABC vuông tại A có đường cao AH ( H ϵ BC)
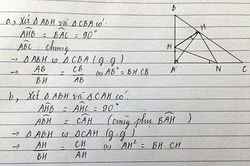
a) chứng minh : △ABC đồng dạng △HAC và AB. AC= AH.BC
b) chứng minh: AC2 = HC.BC
c) chứng minh : AH2= HB.HC
Cho tam giác ABC vuông tại A có AB=6cm,AC=8cm.kẻ đường cao AH (H thuộc BC).Câu a, chứng minh tam giác ABC đồng dạng với tam giác HBA và AB.AC=AH.BC
Câu b, chứng minh AH2=HB.HC
Cho tam giác ABC vuông ở A.Kẻ ba đường cao AH,BK,CM
a) CM: AB.AC=AH.BC?
b) CM: AC2=HC.BC
c) AH2=HB.HC
Cho ∆ABC vuông tại A có AB6cm, AC 8cm, đường cao AHa) Tính BC và AHb) Kẻ HE AB tại E, HF AC tại F. Chứng minh ∆AEH đồng dạng ∆AHBc) Chứng minh AH2 AF.ACd) Chứng minh ∆ABC đồng dạng ∆AFEe) Tính diện tích tứ giác BCFE
Đọc tiếp
Cho ∆ABC vuông tại A có AB=6cm, AC= 8cm, đường cao AH
a) Tính BC và AH
b) Kẻ HE 
AB tại E, HF AC tại F. Chứng minh ∆AEH đồng dạng ∆AHB
c) Chứng minh AH2 = AF.AC
d) Chứng minh ∆ABC đồng dạng ∆AFE
e) Tính diện tích tứ giác BCFE
Cho tam giác ABC vuông tại A, đường cao AH
a) Chứng minh: Tam giác HBA đồng dạng với tam giác ABC và góc BAH = góc BCA
b) Chứng minh AH2 = BH . HC
c) Kẻ phân giác BD của góc ABC ( D thuộc AC ) cắt AH tại E. Cho AB = 15cm, AC = 20cm. Tính BD.
d) Gọi M là trung điểm của ED. Kẻ EF vuông góc với AB tại F. Chứng minh ba đường thẳng EF, BH, AM đồng quy.
21 tháng 3 2023 lúc 20:17
Cho Δ ABC ⊥ tại A. Đường cao AH
a) Chứng minh ΔBHA đồng dạng với ΔBAC
b) Chứng minh \(AH^2=HB.HC\)
Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm. Kẻ đường cao AH. a) Chứng minh: ABC và HBA đồng dạng với nhau b) Chứng minh: AH2 = HB.HC c) Tính độ dài các cạnh BC, AH d) Phân giác của góc ACB cắt AH tại E, cắt AB tại D. Tính tỉ số diện tích của hai tam giác ACD và HCE
20 tháng 5 2022 lúc 5:23
Cho tam giác ABC vuông tại A, biết AB = 6cm, AC = 9 cm. Đường cao AH ( H thuộc BC). a) Chứng minh: HAC đồng dạng ABC b) Chứng minh: AC2 = BC.HC c) Kẻ đường phân giác AD, tính độ dài BD và CD . ( lm r nma sợ sai ;-; )
cho tam giác ABC vuông tại A , đường cao AH
a. Chứng minh DABC đồng dạng với DHBA, từ đó suy ra AB bình= BH.BC
b. Tia phân giác của góc ABC cắt AH tại I, chứng minh rằng IA/IH=AC/HA
c. Tia phân giác của góc HAC cắt BC tại K, chứng minh rằng IK song song với AC