Question

Cho△ ABC có AH là đường cao(HϵBC). Gọi D và E lần lượt là hình chiếu của H trên AB và AC. CMR:

a) △ABH ∼ △ AHD

b)HE² = AE.EC

c) Gọi M là giao điểm của BE và CD. CMR △DBM ∼ △ECM

Answer 1

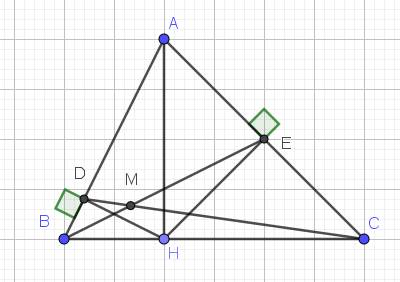
Lời giải:
a. Xét tam giác $ABH$ và $AHD$ có:

$\widehat{A}$ chung

$\widehat{AHB}=\widehat{ADH}=90^0$

$\Rightarrow \triangle ABH\sim \triangle AHD$ (g.g)

b. Xét tam giác $AEH$ và $HEC$ có:
$\widehat{AEH}=\widehat{HEC}=90^0$

$\widehat{EAH}=90^0-\widehat{AHE}=\widehat{EHC}$ 

$\Rightarrow \triangle AEH\sim \triangle HEC$ (g.g)

$\Rightarrow \frac{AE}{EH}=\frac{HE}{EC}$

$\Rightarrow HE^2=AE.EC$

c. Từ $\triangle ABH\sim \triangle AHD$ (phần a) suy ra:
$\frac{AB}{AH}=\frac{AH}{AD}$

$\Rightarrow AH^2=AB.AD$ 

Tương tự ta cũng có thể cm $\triangle AHE\sim \triangle ACH$

$\Rightarrow AH^2=AE.AC$ 

$\Rightarrow AB.AD=AE.AC$

$\Rightarrow \frac{AB}{AE}=\frac{AC}{AD}$

$\Rightarrow \triangle ABE\sim \triangle ACD$ (c.g.c)

$\Rightarrow \widehat{ABE}=\widehat{ACD}$ hay $\widehat{DBM}=\widehat{ECM}$

Xét tam giác $DBM$ và $ECM$ có:

$\widehat{DBM}=\widehat{ECM}$ (cmt) 

$\widehat{DMB}=\widehat{EMC}$ (đối đỉnh)

$\Rightarrow \triangle DBM\sim \triangle ECM$ (g.g)

 

Answer 2

Hình vẽ: