Phương pháp:
Công thức tính thể tích của khối nón có bán kính đá R và chiều cao h: V = 1 3 π R 2 h
Cách giải:
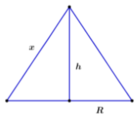
Gọi cạnh của tam giác đều qua trục là x

Phương pháp:
Công thức tính thể tích của khối nón có bán kính đá R và chiều cao h: V = 1 3 π R 2 h
Cách giải:

Gọi cạnh của tam giác đều qua trục là x

Cắt một hình nón bằng một mặt phẳng qua trục của nó được thiết diện là tam giác đểu cạnh bằng a. Tính thể tích V của khối nón theo A
A. V = π a 3 3 12
B. V = π a 3 3 24
C. V = π a 3 3 6
D. V = π a 3 3 3
Cho hình trụ có diện tích xung quanh bằng 4 π , thiết diện qua trục là hình vuông. Tính thể tích V của khối trụ giới hạn bởi hình trụ
A. V = 2 π
B. V = 6 π
C. V = 3 π
D. V = 5 π
Tính thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x = π , biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác đều cạnh là 2 sin x
A. V = 3
B. V = 3 π
C. V = - 2 π 3
D. V = 2 3
Tính thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x = π , biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác đều cạnh là 2 s i n x
A. V = 3
B. V = 3 π
C. V = 2 π 3
D. V = 2 3
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P = R + 2r.
A. 2 3
B. 3
C. 3 3
D. 2
Thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x = π , biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 0 ≤ x ≤ π ) là một tam giác đều cạnh
A. V = 3
B. V = 3 π
C. 2 3
D. 2 π 3
Thiết diện qua trục của hình nón tròn xoay là một tam giác đều cạnh 2a. Tính thể tích V của khối nón đó.
A. V = π a 3 3
B. V = π a 3 3 3
C. V = π a 3 3 24
D. V = 3 π a 3 8
Cắt hình nón bởi một mặt phẳng qua trục ta được thiết diện là một tam giác vuông cân có cạnh huyền bằng a 6 . Tính thể tích V của khối nón đó
A. V = π a 3 6 6
B. V = π a 3 6 3
C. V = π a 3 6 2
D. V = π a 3 6 4
Cắt hình nón bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân có cạnh huyền bằng a 6 . Tính thể tích V của khối nón đó.
A. V = πa 3 6 4
B. V = πa 3 6 2
C. V = πa 3 6 6
D. V = πa 3 6 3