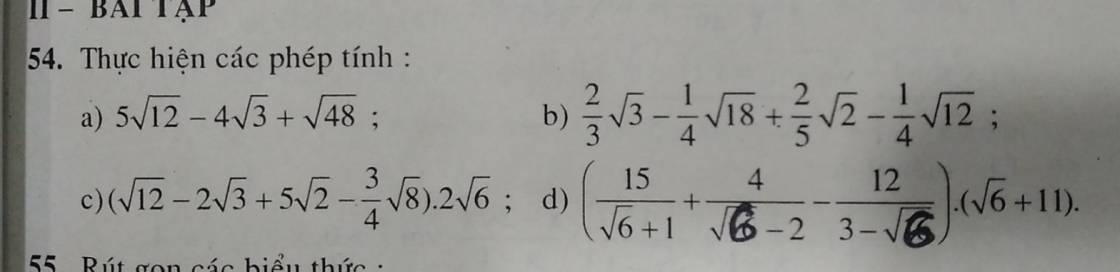a)
\(5\sqrt{12}-4\sqrt{3}+\sqrt{48}\\ =5\sqrt{4.3}-4\sqrt{3}+\sqrt{16.3}\\ =10\sqrt{3}-4\sqrt{3}+4\sqrt{3}\\ =10\sqrt{3}\)
b)
\(\dfrac{2}{3}\sqrt{3}-\dfrac{1}{4}\sqrt{9.2}+\dfrac{2}{5}\sqrt{2}-\dfrac{1}{4}\sqrt{4.3}\\ =\dfrac{2}{3}\sqrt{3}-\dfrac{1}{2}\sqrt{3}-\dfrac{3}{4}\sqrt{2}+\dfrac{2}{5}\sqrt{2}\\ =\left(\dfrac{2}{3}-\dfrac{1}{2}\right)\sqrt{3}-\sqrt{2}\left(\dfrac{3}{4}-\dfrac{2}{5}\right)\\ =\dfrac{1}{6}\sqrt{3}-\dfrac{7}{20}\sqrt{2}\)
c)
\(\left(\sqrt{12}-2\sqrt{3}+5\sqrt{2}-\dfrac{3}{4}\sqrt{8}\right).2\sqrt{6}\\ =\left(\sqrt{4.3}-2\sqrt{3}+5\sqrt{2}-\dfrac{3}{4}\sqrt{4.2}\right).2\sqrt{6}\\ =\left(2\sqrt{3}-2\sqrt{3}+5\sqrt{2}-\dfrac{3}{2}\sqrt{2}\right).2\sqrt{6}\\ =\dfrac{7}{2}\sqrt{2}.2\sqrt{6}\\ =7\sqrt{12}\)
a) \(5\sqrt{12}-4\sqrt{3}+\sqrt{48}\)
\(=5\cdot\sqrt{2^2\cdot3}-4\sqrt{3}+\sqrt{4^2\cdot3}\)
\(=5\cdot2\sqrt{3}-4\sqrt{3}+4\sqrt{3}\)
\(=10\sqrt{3}\)
b) \(\dfrac{2}{3}\sqrt{3}-\dfrac{1}{4}\sqrt{18}+\dfrac{2}{5}\sqrt{2}-\dfrac{1}{4}\sqrt{12}\)
\(=\dfrac{2}{3}\sqrt{3}-\dfrac{1}{4}\sqrt{3^2\cdot2}+\dfrac{2}{5}\sqrt{2}-\dfrac{1}{4}\sqrt{2^2\cdot3}\)
\(=\dfrac{2}{3}\sqrt{3}-\dfrac{1}{4}\cdot3\sqrt{2}+\dfrac{2}{5}\sqrt{2}-\dfrac{1}{4}\cdot2\sqrt{3}\)
\(=\dfrac{2}{3}\sqrt{3}-\dfrac{3}{4}\sqrt{2}+\dfrac{2}{5}\sqrt{2}-\dfrac{1}{2}\sqrt{3}\)
\(=\left(\dfrac{2}{3}-\dfrac{1}{2}\right)\sqrt{3}-\left(\dfrac{3}{4}-\dfrac{2}{5}\right)\sqrt{2}\)
\(=\dfrac{1}{6}\sqrt{3}-\dfrac{7}{20}\sqrt{2}\)
\(=\dfrac{\sqrt{3}}{6}-\dfrac{7\sqrt{2}}{20}\)
c) \(\left(\sqrt{12}-2\sqrt{3}+5\sqrt{2}-\dfrac{3}{4}\sqrt{8}\right)\cdot2\sqrt{6}\)
\(=\left(2\sqrt{3}-2\sqrt{3}+5\sqrt{2}-\dfrac{3}{4}\cdot2\sqrt{2}\right)\cdot2\sqrt{6}\)
\(=\left(5\sqrt{2}-\dfrac{3}{2}\sqrt{2}\right)\cdot2\sqrt{6}\)
\(=\dfrac{7}{2}\sqrt{2}\cdot2\sqrt{6}\)
\(=14\sqrt{3}\)
d) \(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right)\cdot\left(\sqrt{6}+11\right)\)
\(=\left[\dfrac{15\left(\sqrt{6}-1\right)}{\left(\sqrt{6}-1\right)\left(\sqrt{6}+1\right)}+\dfrac{4\left(\sqrt{6}+2\right)}{\left(\sqrt{6}-2\right)\left(\sqrt{6}+2\right)}-\dfrac{12\left(3+\sqrt{6}\right)}{\left(3+\sqrt{6}\right)\left(3-\sqrt{6}\right)}\right]\left(\sqrt{6}+11\right)\)
\(=\left[\dfrac{15\left(\sqrt{6}-1\right)}{5}+\dfrac{4\left(\sqrt{6}+2\right)}{2}-\dfrac{12\left(3+\sqrt{6}\right)}{3}\right]\left(\sqrt{6}+11\right)\)
\(=\left(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}\right)\left(\sqrt{6}+11\right)\)
\(=\left(\sqrt{6}-11\right)\left(\sqrt{6}+11\right)\)
\(=6-121\)
\(=-115\)
\(a,5\sqrt{12}-4\sqrt{3}+\sqrt{48}\)
\(=5\sqrt{4\cdot3}-4\sqrt{3}+\sqrt{16\cdot3}\)
\(=5\cdot2\sqrt{3}-4\sqrt{3}+4\sqrt{3}\)
\(=10\sqrt{3}\)
\(---\)
\(b,\dfrac{2}{3}\sqrt{3}-\dfrac{1}{4}\sqrt{18}+\dfrac{2}{5}\sqrt{2}-\dfrac{1}{4}\sqrt{12}\)
\(=\dfrac{2}{3}\sqrt{3}-\dfrac{1}{4}\sqrt{9\cdot2}+\dfrac{2}{5}\sqrt{2}-\dfrac{1}{4}\sqrt{4\cdot3}\)
\(=\dfrac{2}{3}\sqrt{3}-\dfrac{1}{4}\cdot3\sqrt{2}+\dfrac{2}{5}\sqrt{2}-\dfrac{1}{4}\cdot2\sqrt{3}\)
\(=\left(\dfrac{2}{3}\sqrt{3}-\dfrac{1}{2}\sqrt{3}\right)+\left(-\dfrac{3}{4}\sqrt{2}+\dfrac{2}{5}\sqrt{2}\right)\)
\(=\dfrac{1}{6}\sqrt{3}-\dfrac{7}{20}\sqrt{2}\)
\(=\dfrac{\sqrt{3}}{6}-\dfrac{7\sqrt{2}}{20}\)
\(---\)
\(c,\left(\sqrt{12}-2\sqrt{3}+5\sqrt{2}-\dfrac{3}{4}\sqrt{8}\right)\cdot2\sqrt{6}\)
\(=\left(\sqrt{4\cdot3}-2\sqrt{3}+5\sqrt{2}-\dfrac{3}{4}\cdot\sqrt{4\cdot2}\right)\cdot2\sqrt{6}\)
\(=\left(2\sqrt{3}-2\sqrt{3}+5\sqrt{2}-\dfrac{3}{2}\sqrt{2}\right)\cdot2\sqrt{6}\)
\(=\dfrac{7}{2}\sqrt{2}\cdot2\sqrt{6}\)
\(=7\cdot\sqrt{2}\cdot\sqrt{6}\)
\(=7\cdot\sqrt{2}\cdot\sqrt{2}\cdot\sqrt{3}\)
\(=14\sqrt{3}\)
\(---\)
\(d,\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right)\cdot\left(\sqrt{6}+11\right)\)
\(=\left[\dfrac{15\cdot\left(\sqrt{6}-1\right)}{\left(\sqrt{6}-1\right)\left(\sqrt{6}+1\right)}+\dfrac{4\left(\sqrt{6}+2\right)}{\left(\sqrt{6}-2\right)\left(\sqrt{6}+2\right)}+\dfrac{12\left(\sqrt{6}+3\right)}{\left(\sqrt{6}-3\right)\left(\sqrt{6}+3\right)}\right]\cdot\left(\sqrt{6}+11\right)\)
\(=\left[\dfrac{15\cdot\left(\sqrt{6}-1\right)}{6-1}+\dfrac{4\left(\sqrt{6}+2\right)}{6-4}+\dfrac{12\left(\sqrt{6}+3\right)}{6-9}\right]\left(\sqrt{6}+11\right)\)
\(=\left[3\left(\sqrt{6}-1\right)+2\left(\sqrt{6}+2\right)-4\left(\sqrt{6}+3\right)\right]\left(\sqrt{6}+11\right)\)
\(=\left(3\sqrt{6}-3+2\sqrt{6}+4-4\sqrt{6}-12\right)\left(\sqrt{6}+11\right)\)
\(=\left(\sqrt{6}-11\right)\left(\sqrt{6}+11\right)\)
\(=6-121\)
\(=-115\)
#\(Toru\)
d)
\(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right).\left(\sqrt{6}+11\right)\\ =\left(\dfrac{15\left(\sqrt{6}-1\right)}{6-1}+\dfrac{4\left(\sqrt{6}+2\right)}{6-4}-\dfrac{12\left(3+\sqrt{6}\right)}{9-6}\right).\left(\sqrt{6}+11\right)\\ =[3\left(\sqrt{6}-1\right)+2\left(\sqrt{6}+2\right)-4\left(3+\sqrt{6}\right)].\left(\sqrt{6}+11\right)\\ =\left(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}\right)\left(\sqrt{6}+11\right)\\ =\left(\sqrt{6}-11\right)\left(\sqrt{6}+11\right)\\ =6-121=-115\)