🎉 THÔNG BÁO THAM GIA SINH HOẠT CÙNG CLB SẮC MÀU 🎉
Xin chào các bạn lại là CLB Sắc Màu đây, lần này CLB Sắc Màu tổ chức sinh hoạt buổi thứ ba với nhiều hoạt động thú vị. Qua đó cũng rất nhiều phần quà hấp dẫn và thú vị đang chờ chủ nhân tại buổi sinh hoạt. Chi tiết chương trình như sau:
Nội dung buổi sinh hoạt gồm bốn phần:
🏖️ Phần 1. Trò chơi nối từ (5đ - với người thắng, 2đ - đối với người thua/1 lượt)
🌸 Phần 2. Trao đổi chia sẻ (3đ/1 lượt). Người tham gia mời bất kỳ một người trong buổi sinh hoạt để đưa ra những thắc mắc hoặc những điều mà mình muốn đối phương chia sẻ. Hoặc tự chia sẻ câu chuyện của chính mình. Vì vậy hãy chuẩn bị những câu hỏi hoặc câu chuyện của chính mình để cùng chia sẻ trong buổi sinh hoạt sắp tới nha!!
🤹♂️Phần 3. Ca hát (5đ/1 lượt). Phần rất sôi động trong 2 buổi sinh hoạt qua nên hãy chuẩn bị một bài hát thật hay để tỏa sáng trong đêm sinh hoạt nhé.
🔥 Phần 4. Xem video, trả lời tên nhân vật. (5đ/1 lượt)
📌Đặc biệt mở camera khi tham gia buổi sinh hoạt, sẽ được +20đ. Buổi sinh hoạt phần lớn cần microphone để tham gia trao đổi, nên mọi người chuẩn bị thiết bị có đầy đủ chức năng để có thể đạt được giải cao nhất nha.
🏆Giải thưởng:
🌟 GIẢI ĐẶC BIỆT: Một quyển sách giúp rèn luyện tư duy hoặc 2 vé xem phim tại rạp.
🥇 1 GIẢI NHẤT: 100 coin
🥈 1 GIẢI NHÌ: 50 coin
🎖5 GIẢI BA: 10 GP
3 BAO LÌ XÌ MỆNH GIÁ NGẪU NHIÊN (Dành cho bạn có bạn chưa đạt giải cao nhưng có phần tham gia ấn tượng)
🎲 BÁNH XE MAY MẮN - ẴM GIẢI ĐẶC BIỆT
Các bạn tham gia trong buổi sinh hoạt sẽ được điền tên trong vòng quay may mắn. Với mỗi bạn tham gia (từ đầu đến cuối buổi sinh hoạt) sẽ có tên trong vòng quay cùng với ô Chúc bạn may mắn lần sau. Ví dụ buổi sinh hoạt có 10 bạn, thì vòng quay sẽ có 20 ô (gồm tên 10 bạn và 10 ô Chúc bạn may mắn lần sau).
Mỗi thành viên tham gia giải đặc biệt cần thực hiện với các điều kiện:
1️⃣ Gửi lời chúc may mắn để mọi người đạt được phần thưởng trong buổi sinh hoạt. (Để đăng ký tham gia sinh hoạt)
2️⃣ Tham gia nhóm chat trên Messenger: https://m.me/j/AbaObDasprtRi3Zh/
⏳Thời gian sinh hoạt: 20:00 ngày 22/2/2025
⏰Thời gian báo danh, giao lưu: 20:00 -> 20:10
Hãy nhanh tay đăng ký và chuẩn bị cho một buổi sinh hoạt đầy sắc màu, sáng tạo và vui nhộn! Hẹn gặp lại các bạn tại CLB Sắc Màu!
“Câu Lạc Bộ Sắc Màu – Nơi tài năng hội tụ, sáng tạo tỏa sáng!” 🌈
----------------------------------------------------------------------------
📥Fanpage: https://www.facebook.com/clbsacmauhoc24
📧Email: [sacmauhoc24@gmail.com]


















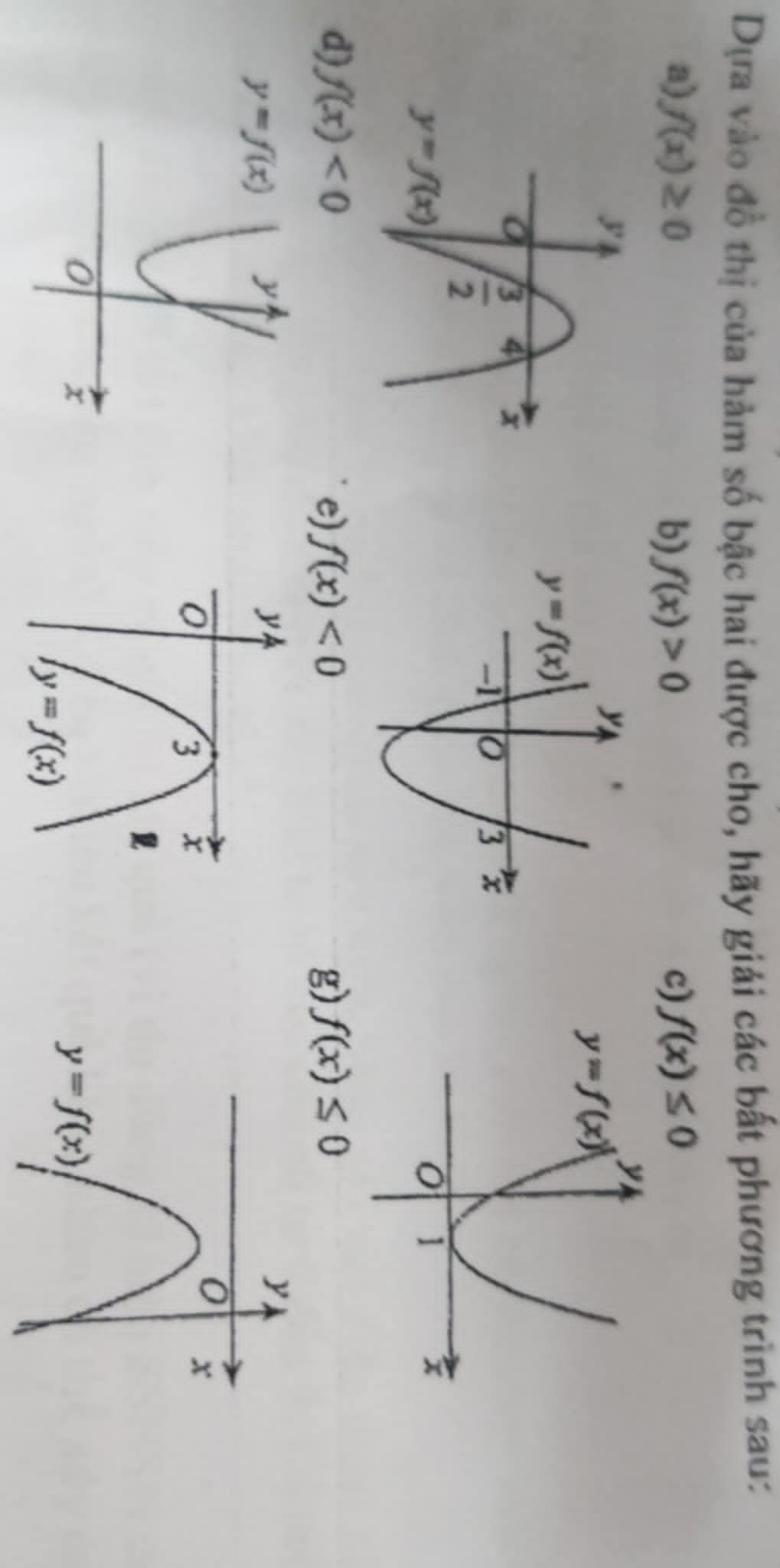

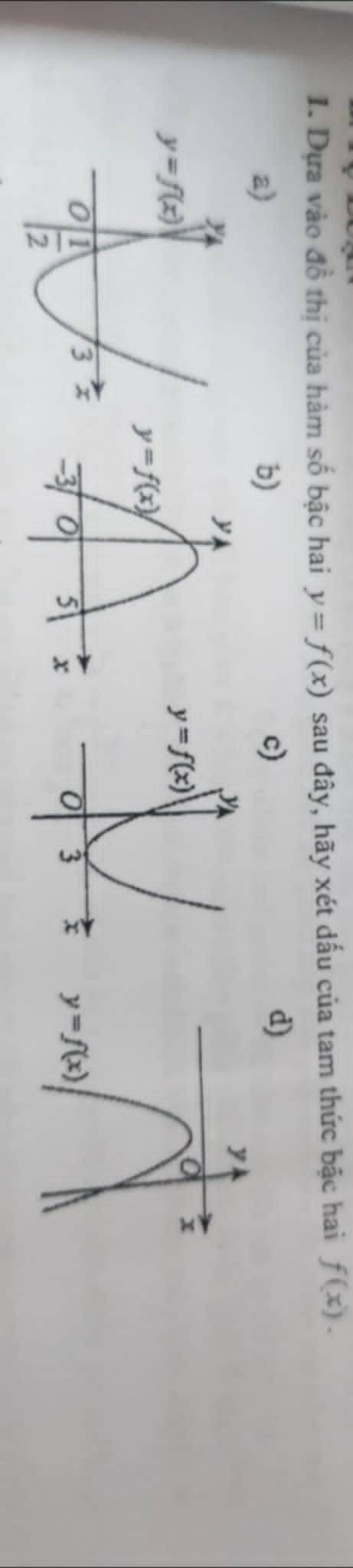

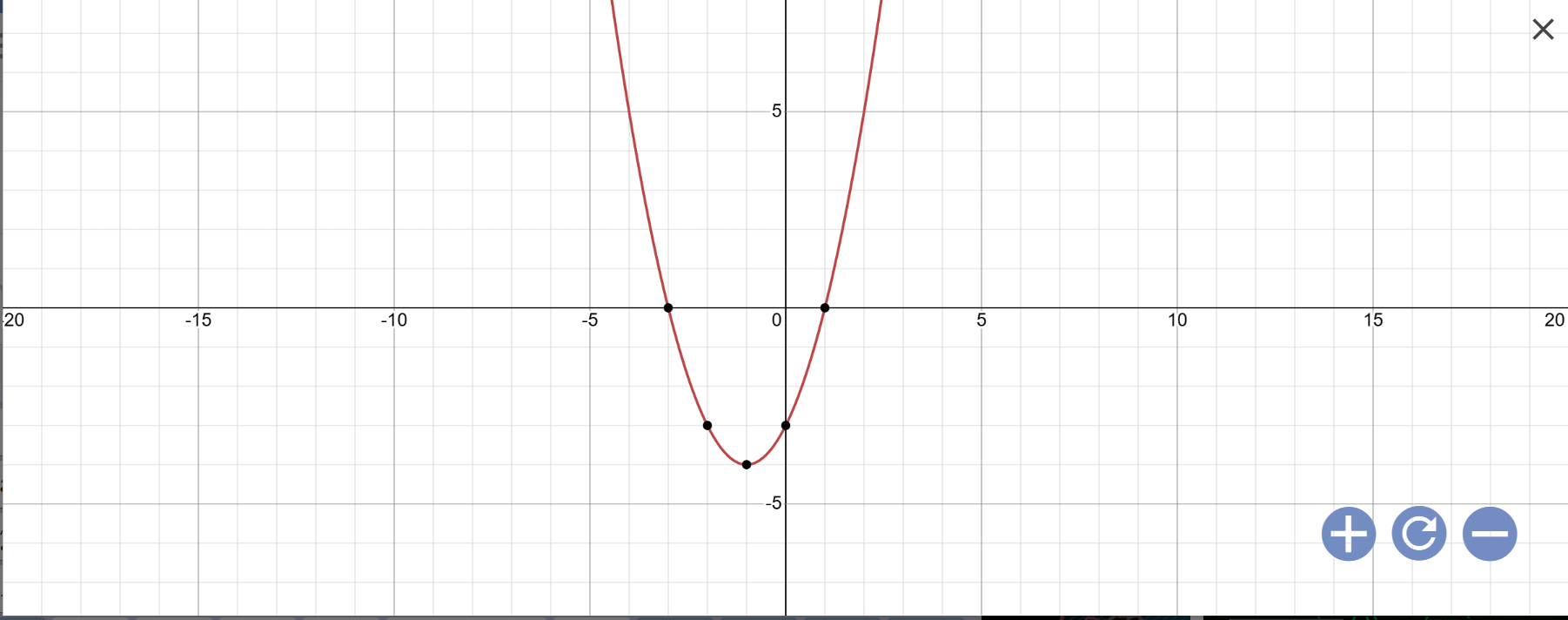
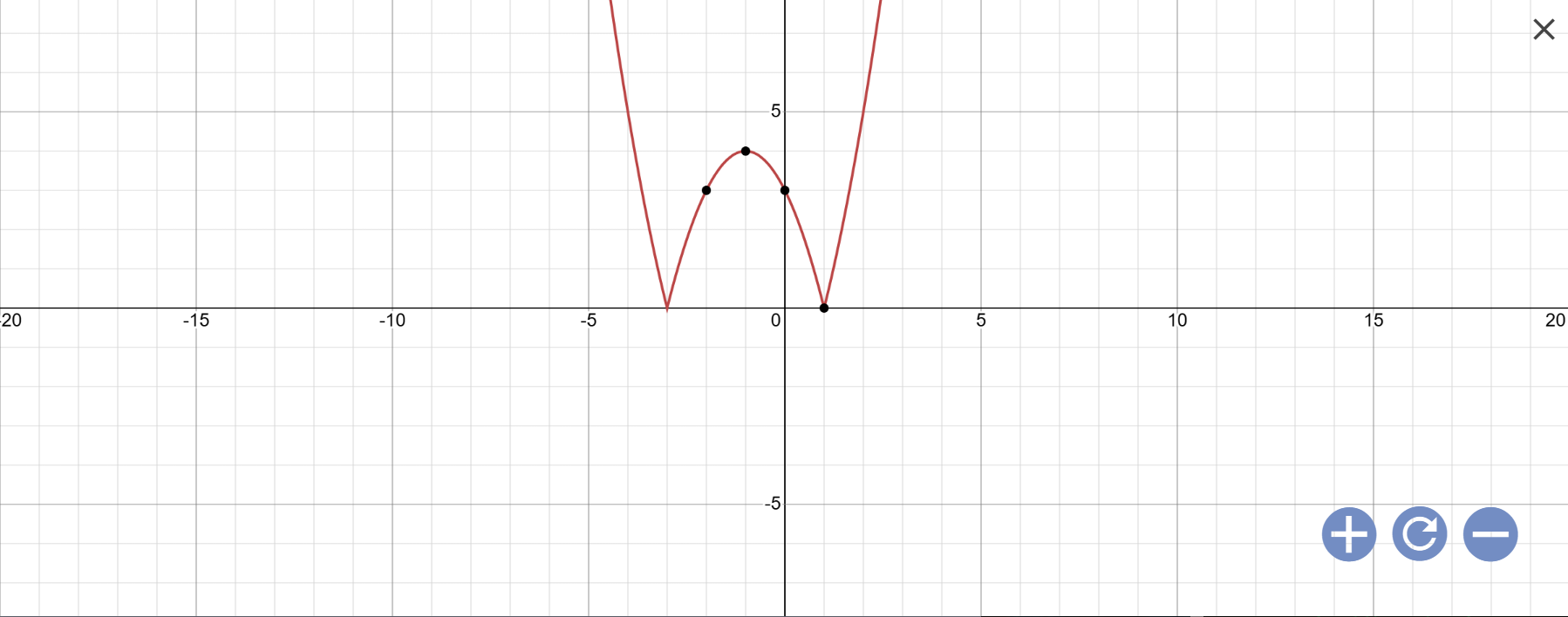
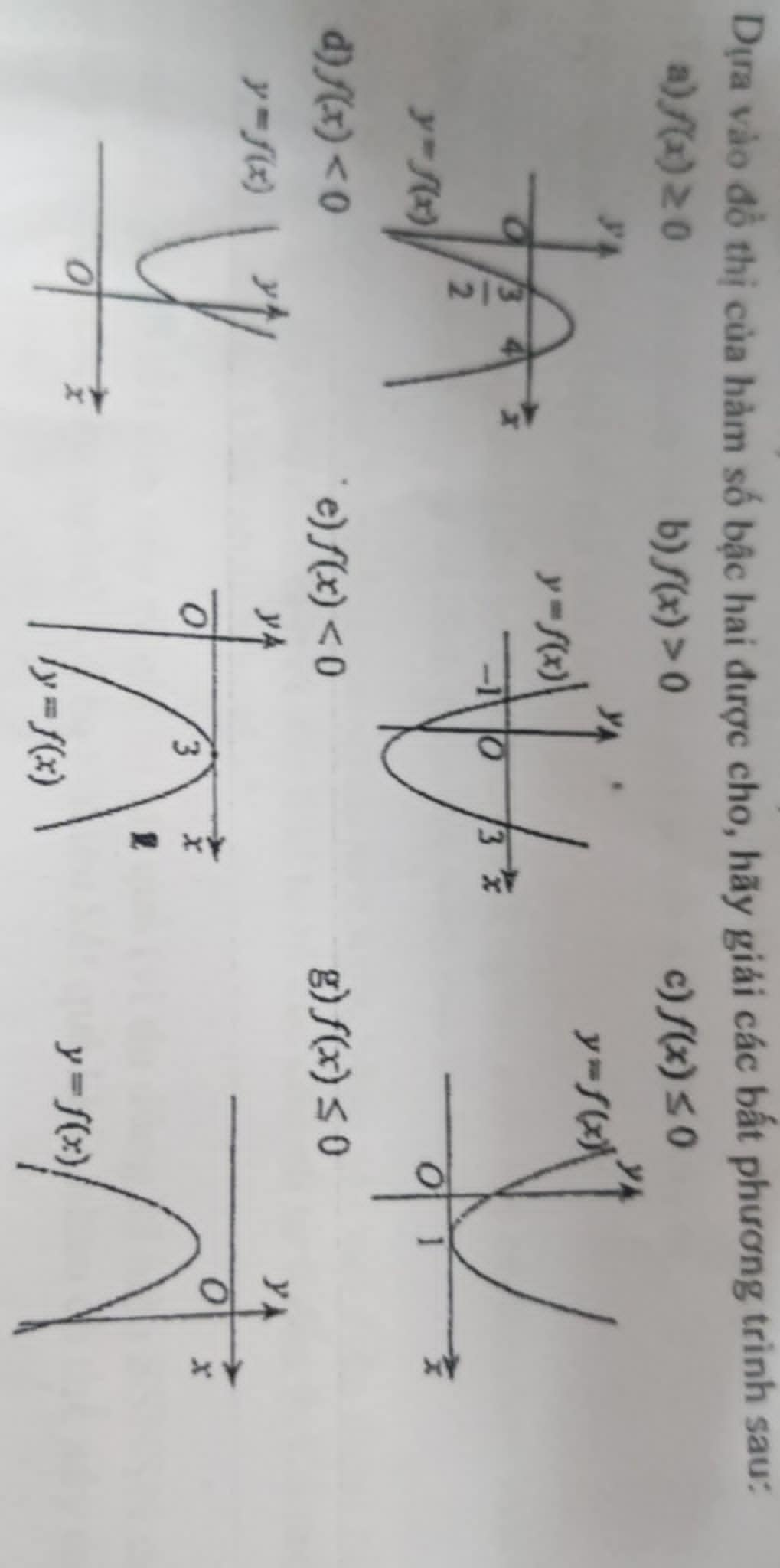
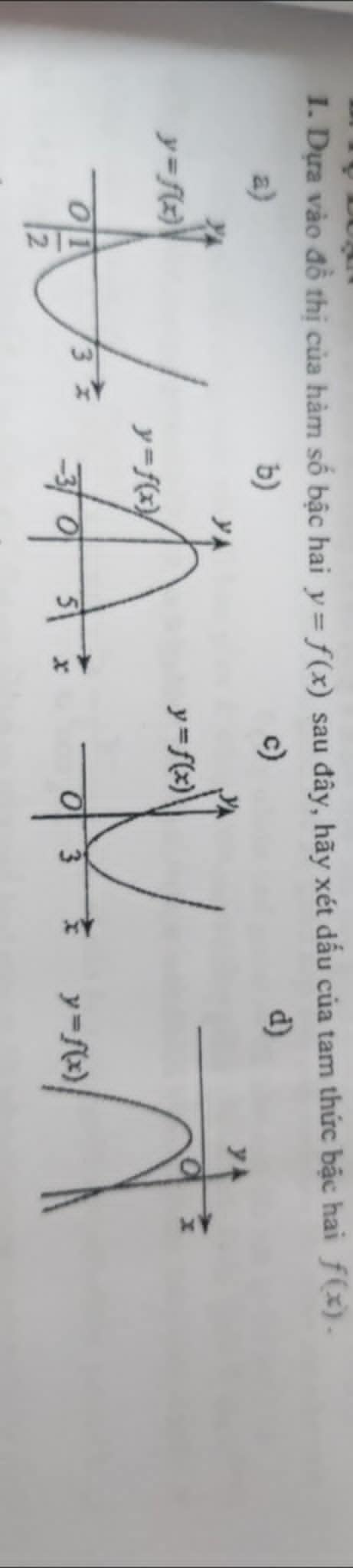
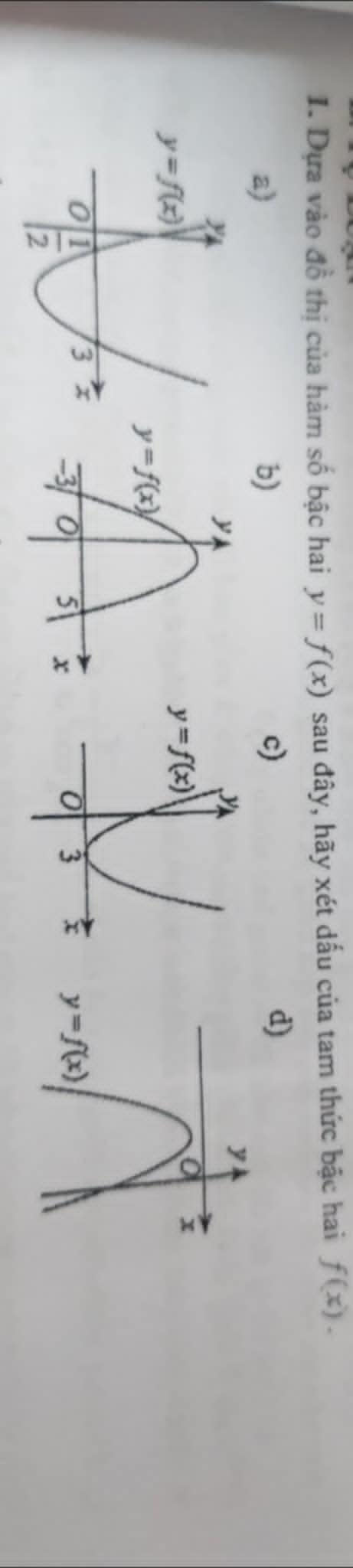 cái này giải sao vậy mn
cái này giải sao vậy mn