Tính giá trị biểu thức: A = \(sin\left(x+14^o\right).sin\left(x+74^o\right)+sin\left(x-76^o\right).sin\left(x-16^o\right)\)
Có cách bấm máy tính không nhỉ mn?
Cái này khỏi bấm máy đi bạn
\(A=sin\left(x+14^0\right)\cdot sin\left(x+74^0\right)+sin\left(x-76^0\right)\cdot sin\left(x-16^0\right)\)
\(=\dfrac{1}{2}\cdot\left[cos\left(x+14^0-x-74^0\right)-cos\left(x+14^0+x+74^0\right)\right]+\dfrac{1}{2}\cdot\left[cos\left(x-76^0-x+16^0\right)-cos\left(x-76^0+x-16^0\right)\right]\)
\(=\dfrac{1}{2}\left[cos\left(-60^0\right)-cos\left(2x+88^0\right)\right]+\dfrac{1}{2}\cdot\left[cos\left(-60^0\right)-cos\left(2x-92^0\right)\right]\)
\(=\dfrac{1}{2}\cdot cos60^0-\dfrac{1}{2}\cdot cos\left(2x+88^0\right)+\dfrac{1}{2}\cdot cos60^0-\dfrac{1}{2}\cdot cos\left(2x-92^0\right)\)
\(=cos60^0-\dfrac{1}{2}\left[cos\left(2x+88^0\right)-cos\left(2x-92^0\right)\right]\)
\(=\dfrac{1}{2}-\dfrac{1}{2}\cdot\left[-2\cdot\sin\left(\dfrac{2x+88^0+2x-92^0}{2}\right)\cdot sin\left(\dfrac{2x+88^0-2x+92^0}{2}\right)\right]\)
\(=\dfrac{1}{2}-\dfrac{1}{2}\cdot\left[-2\cdot sin\left(2x-2^0\right)\cdot sin\left(\dfrac{180^0}{2}\right)\right]\)
\(=\dfrac{1}{2}-\dfrac{1}{2}\cdot\left[-2\cdot sin\left(2x-2^0\right)\cdot sin90^0\right]\)
\(=\dfrac{1}{2}+\dfrac{1}{2}\cdot2\cdot sin\left(2x-2^0\right)=sin\left(2x-2^0\right)+\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
mọi người giải giúp em vd này với ạ

mọi người giúp em giải câu vd này với ạ

mọi người giúp em giải bt5 với ạ
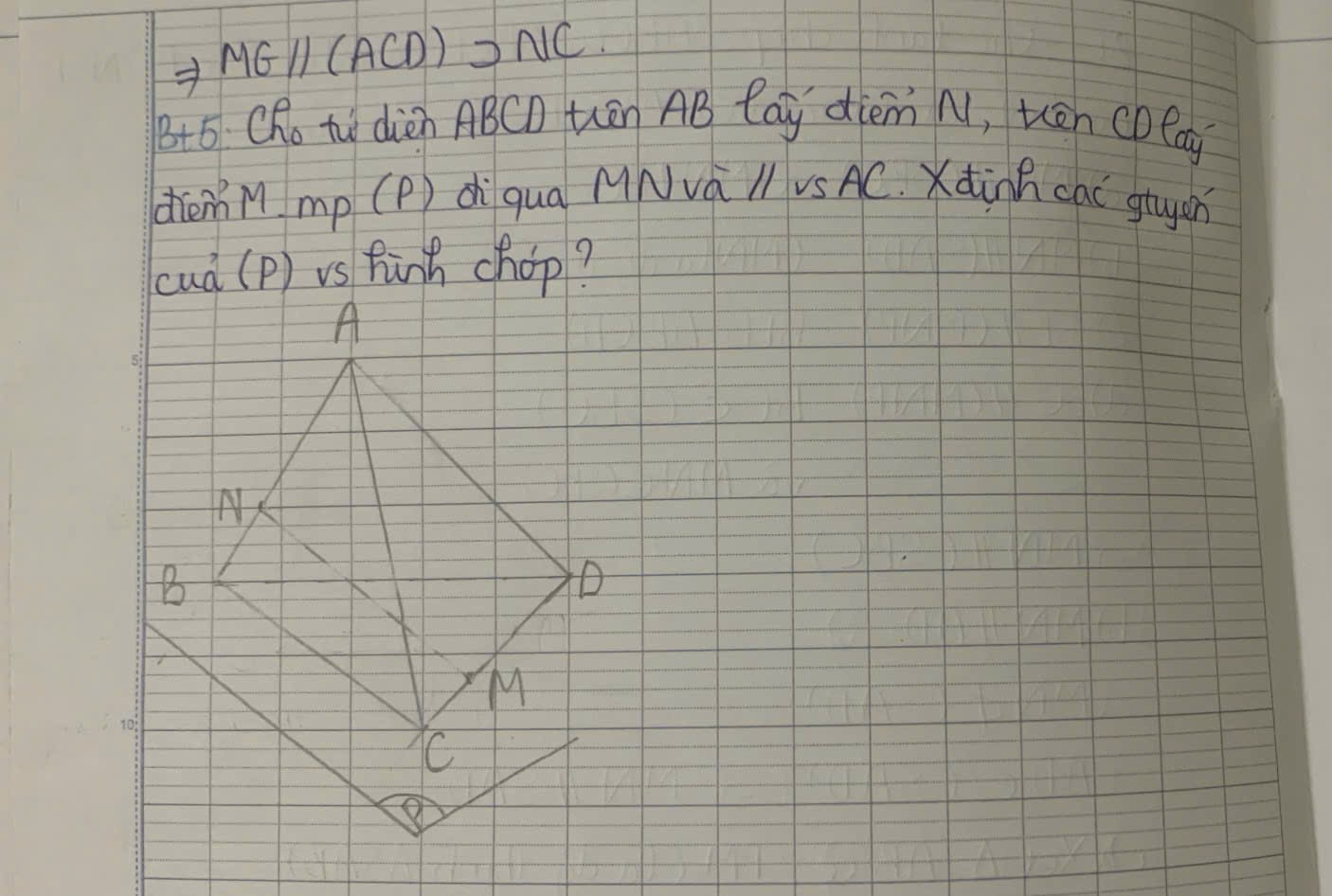
Cho em lời giải chi tiết nhé + vẽ hình cho em nữa nha Em cảm ơn ạ

Ai giúp em giải chi tiết câu 16 với ạ

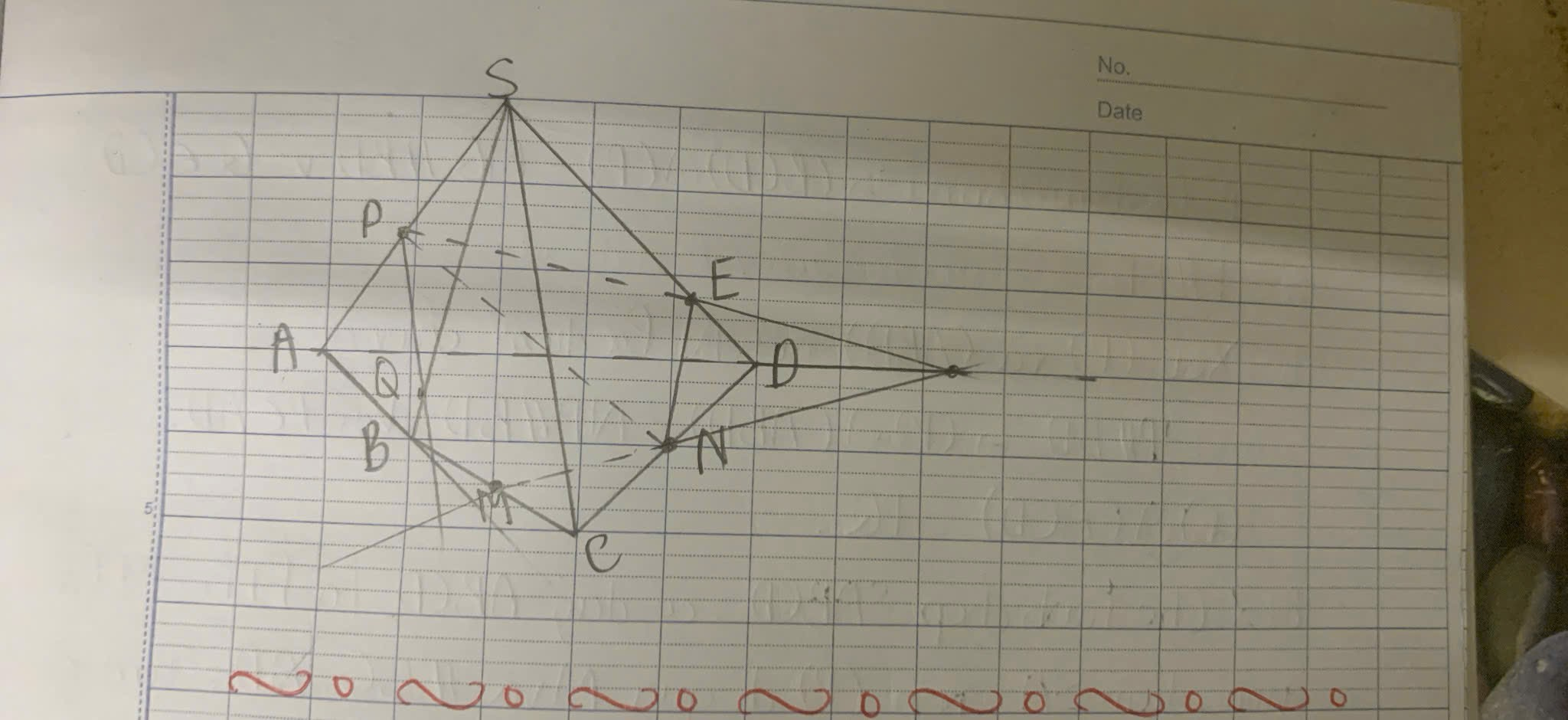
Làm chi tiết cho em với ạ

34.
Câu này đề bài thiếu, cần có thêm dữ kiện khác về (P) nữa mới kết luận được, chứ ở đây hoàn toàn ko có bất cứ ràng buộc nào về (P) cả, thì thậm chí nó có thể ko cắt hộp, hoặc chỉ cắt ở 1 điểm, hoặc cắt theo thiết diện là tam giác, tứ giác, ngũ giác, lục giác đều được
35. D đúng
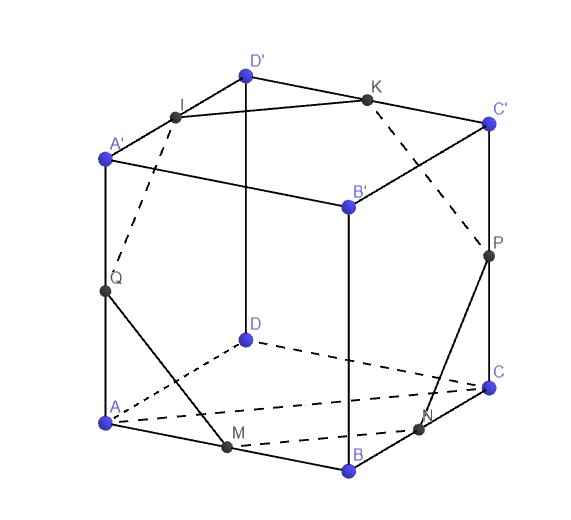
Gọi Q là trung điểm AA', I là trung điểm A'D', K là trung điểm C'D'
M là trung điểm AB, N là trung điểm BC nên MN là đường trung bình tam giác ABC
\(\Rightarrow MN||AC\)
P là trung điểm CC', Q là trung điểm AA' nên \(PQ||AC\Rightarrow MN||PQ\)
\(\Rightarrow Q\in\left(MNP\right)\)
Tương tự ta có \(\left\{{}\begin{matrix}QI||AD'\\NP||BC'\end{matrix}\right.\) (đường trung bình)
Mà \(AD'||BC'\) theo t/c lập phương \(\Rightarrow QI||NP\Rightarrow I\in\left(MNP\right)\)
\(IK||A'C'\) (đường trung bình) \(\Rightarrow IK||AC\Rightarrow IK||MN\Rightarrow K\in\left(MNP\right)\)
Do đó (MNP) cắt lập phương theo lục giác MNPKIQ
Đúng 1
Bình luận (0)
Cho em lời giải chi tiết nhé + vẽ hình cho em nữa nha Em cảm ơn ạ .Em làm được câu 32 rồi ạ
Đọc tiếp
Cho em lời giải chi tiết nhé + vẽ hình cho em nữa nha Em cảm ơn ạ .
Em làm được câu 32 rồi ạ

30. Em khoanh đúng rồi (đơn giản là sử dụng t/c một mặt phẳng cắt 2 mặt phẳng song song thì 2 giao tuyến cũng song song).
31. Em khoanh đúng rồi.
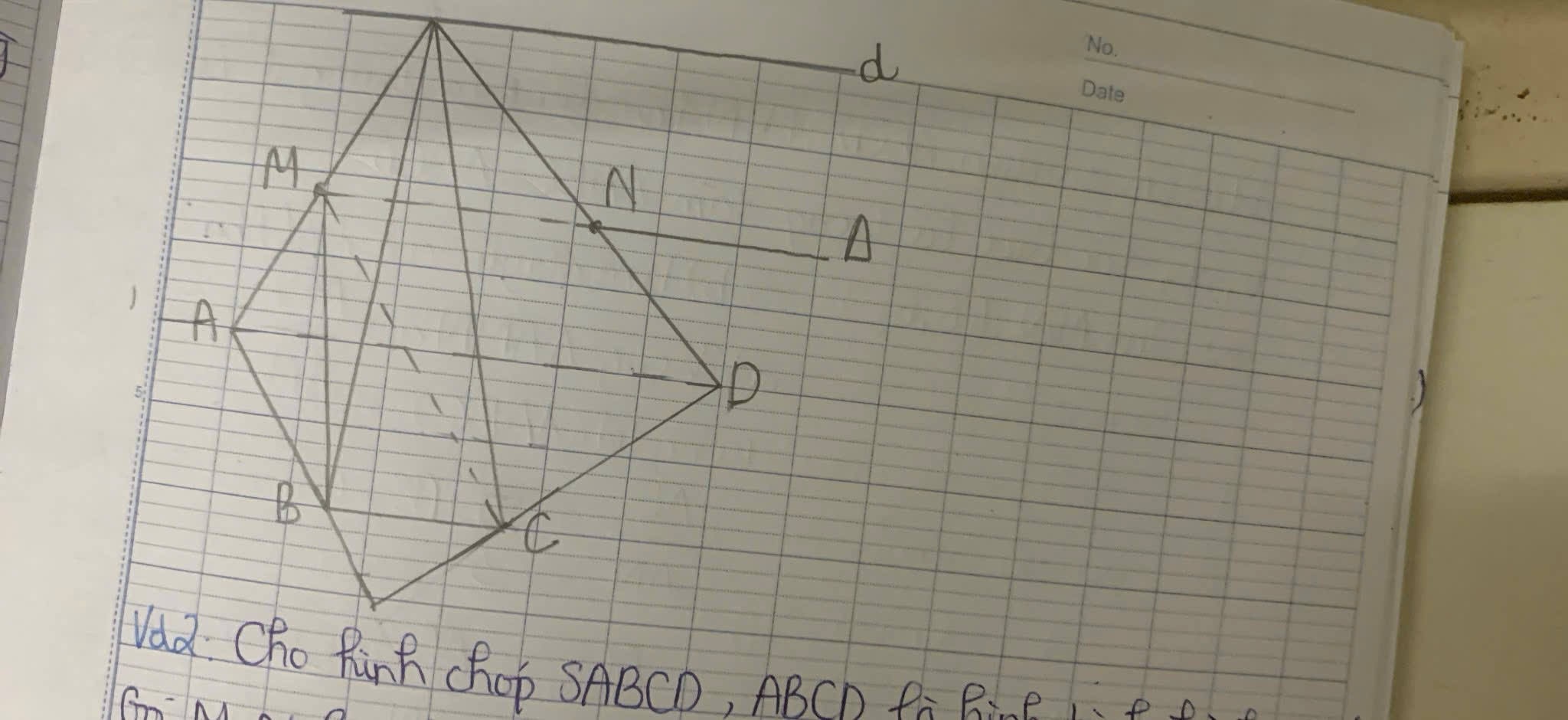
Qua M kẻ đường thẳng song song CD cắt AC tại E
Qua N kẻ đường thẳng song song CD cắt BD tại F
\(\Rightarrow MENF\) là thiết diện của (P) và tứ diện
\(ME||NF\) (cùng song song CD) nên MENF là hình thang
Theo định lý Thales: \(\dfrac{ME}{CD}=\dfrac{AM}{AD}=\dfrac{1}{3}\) (1)
Theo giả thiết \(\dfrac{NC}{BC}=\dfrac{1}{3}\Rightarrow\dfrac{NB}{BC}=\dfrac{2}{3}\)
Theo định lý Thales: \(\dfrac{NF}{CD}=\dfrac{BN}{BC}=\dfrac{2}{3}\) (2)
(1);(2) \(\Rightarrow NF=2ME\)
Đúng 1
Bình luận (0)
32. B đúng
\(\left\{{}\begin{matrix}S\in\left(SAD\right)\cap\left(SBC\right)\\AD\in\left(SAD\right);BC\in\left(SBC\right)\\AD||BC\end{matrix}\right.\)
\(\Rightarrow\left(SAD\right)\cap\left(SBC\right)=Sx||AD||BC\)
33. B đúng
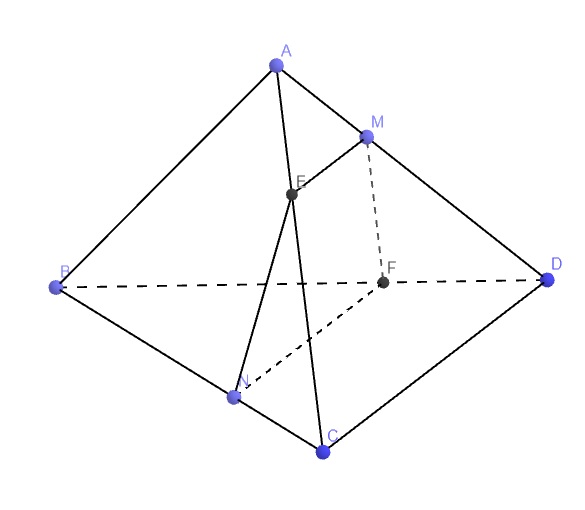
Qua M kẻ đường thẳng song song IC cắt AC tại N
Qua M kẻ đường thẳng song song SI cắt SA tại P
\(\Rightarrow MNP\) là thiết diện của \(\left(\alpha\right)\) là SABC.
Do SABC là tứ diện đều \(\Rightarrow SI=CI\)
Theo định lý Thales: \(\left\{{}\begin{matrix}\dfrac{MN}{CI}=\dfrac{AM}{AI}\\\dfrac{MP}{SI}=\dfrac{AM}{AI}\end{matrix}\right.\)
\(\Rightarrow MN=MP\)
\(\Rightarrow\Delta MNP\) cân tại M
Đúng 1
Bình luận (0)
Xem thêm câu trả lời