30. Em khoanh đúng rồi (đơn giản là sử dụng t/c một mặt phẳng cắt 2 mặt phẳng song song thì 2 giao tuyến cũng song song).
31. Em khoanh đúng rồi.
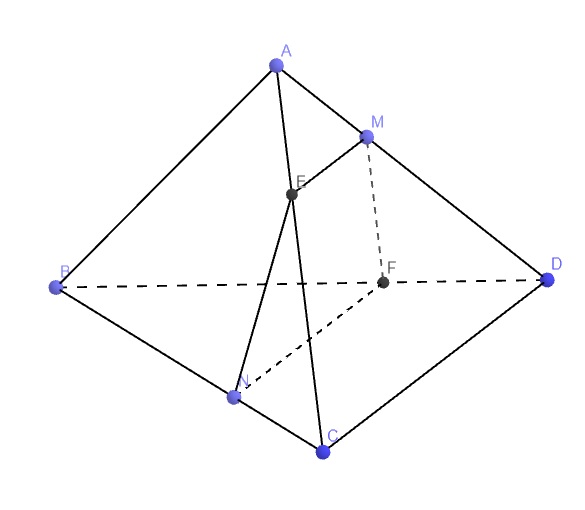
Qua M kẻ đường thẳng song song CD cắt AC tại E
Qua N kẻ đường thẳng song song CD cắt BD tại F
\(\Rightarrow MENF\) là thiết diện của (P) và tứ diện
\(ME||NF\) (cùng song song CD) nên MENF là hình thang
Theo định lý Thales: \(\dfrac{ME}{CD}=\dfrac{AM}{AD}=\dfrac{1}{3}\) (1)
Theo giả thiết \(\dfrac{NC}{BC}=\dfrac{1}{3}\Rightarrow\dfrac{NB}{BC}=\dfrac{2}{3}\)
Theo định lý Thales: \(\dfrac{NF}{CD}=\dfrac{BN}{BC}=\dfrac{2}{3}\) (2)
(1);(2) \(\Rightarrow NF=2ME\)
32. B đúng
\(\left\{{}\begin{matrix}S\in\left(SAD\right)\cap\left(SBC\right)\\AD\in\left(SAD\right);BC\in\left(SBC\right)\\AD||BC\end{matrix}\right.\)
\(\Rightarrow\left(SAD\right)\cap\left(SBC\right)=Sx||AD||BC\)
33. B đúng
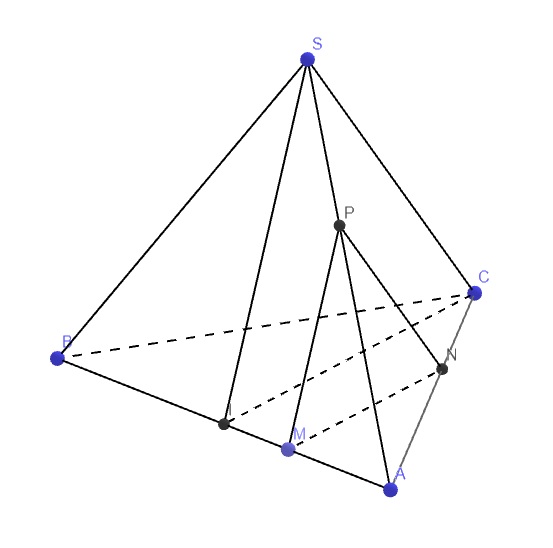
Qua M kẻ đường thẳng song song IC cắt AC tại N
Qua M kẻ đường thẳng song song SI cắt SA tại P
\(\Rightarrow MNP\) là thiết diện của \(\left(\alpha\right)\) là SABC.
Do SABC là tứ diện đều \(\Rightarrow SI=CI\)
Theo định lý Thales: \(\left\{{}\begin{matrix}\dfrac{MN}{CI}=\dfrac{AM}{AI}\\\dfrac{MP}{SI}=\dfrac{AM}{AI}\end{matrix}\right.\)
\(\Rightarrow MN=MP\)
\(\Rightarrow\Delta MNP\) cân tại M