Có bạn nào muốn chơi Minigame nhận quà KHỦNG là tiền mặt hông??
Ai muốn chơi C.M.T "sẵn sàng"! Tối cô lên bài nhé! 😁
Xem thêm câu trả lời
Xin chào HOC24.VNThông báo kết thúc việc đăng câu hỏi SGK mới lớp 6.Chào thành viên box toán , mình đã hoàn thiện xong 1 bộ sách cuối môn toán lớp 6 . Mình sẽ sang bộ sách Cánh Diều lớp 7 từ ngày 28/10/2022 .Rất cảm mơn các bạn đã ủng hộ . Nếu có ý kiến gì hãy bình luận bên dưới nha # HOC24.VN
Đọc tiếp
Xin chào HOC24.VN
Thông báo kết thúc việc đăng câu hỏi SGK mới lớp 6.
Chào thành viên box toán , mình đã hoàn thiện xong 1 bộ sách cuối môn toán lớp 6 . Mình sẽ sang bộ sách Cánh Diều lớp 7 từ ngày 28/10/2022 .
Rất cảm mơn các bạn đã ủng hộ . Nếu có ý kiến gì hãy bình luận bên dưới nha
# HOC24.VN

ủa sao ko cho chân trời sáng tạo chán
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Hoc24.vn chúc mừng các bạn đã đạt giải thưởng tháng 9.Danh sách: https://hoc24.vn/tin-tuc/giai-thuong-hoi-dap-hang-thang-danh-cho-thanh-vien-tich-cuc-192022-1102022.htmlCác bạn nhắn tin ngay cho cô thông tin nhận quà nhé: Tên người nhận- Số điện thoại- Địa chỉ- Món quà muốn nhận.Chúc tất cả các em có một tháng học tập hiệu quả 3
Đọc tiếp

Hoc24.vn chúc mừng các bạn đã đạt giải thưởng tháng 9.
Danh sách: https://hoc24.vn/tin-tuc/giai-thuong-hoi-dap-hang-thang-danh-cho-thanh-vien-tich-cuc-192022-1102022.html
Các bạn nhắn tin ngay cho cô thông tin nhận quà nhé: Tên người nhận- Số điện thoại- Địa chỉ- Món quà muốn nhận.
Chúc tất cả các em có một tháng học tập hiệu quả <3
Này phải là giải thưởng tháng 9 mới đúng chứ ạ?
Đúng 5
Bình luận (1)
Xem thêm câu trả lời
Hoc24 xin chúc mừng các bạn sau đã nhận được phần thưởng dành cho thành viên tích cực:Môn Toán: Lê Michael Môn Vật lý: Dzịt Môn Hóa học: ๖ۣۜDũ๖ۣۜN๖ۣۜG Môn Ngữ văn: Tuệ Lâm Đỗ Môn Tiếng anh: Khinh YênMôn Tiếng anh: _silverliningMôn Tin học: Nguyễn Lê Phước ThịnhCác bạn nhắn tin ngay thông tin nhận thưởng cho cô nhé.Quà tặng: Áo phông, mũ hoặc túi rút.Thông tin: Tên, số điện thoại, địa chỉ chi tiết của người nhận.Cảm ơn các em.
Đọc tiếp

Hoc24 xin chúc mừng các bạn sau đã nhận được phần thưởng dành cho thành viên tích cực:
Môn Toán: Lê Michael
Môn Vật lý: Dzịt
Môn Hóa học: ๖ۣۜDũ๖ۣۜN๖ۣۜG
Môn Ngữ văn: Tuệ Lâm Đỗ
Môn Tiếng anh: Khinh Yên
Môn Tiếng anh: _silverlining
Môn Tin học: Nguyễn Lê Phước Thịnh
Các bạn nhắn tin ngay thông tin nhận thưởng cho cô nhé.
Quà tặng: Áo phông, mũ hoặc túi rút.
Thông tin: Tên, số điện thoại, địa chỉ chi tiết của người nhận.
Cảm ơn các em.
Xem thêm câu trả lời
⚡ Tặng các em playlist nhạc để tập trung khi học bài và cũng thư giãn nữa nhé!❉ Hãy nghe và comment cho cô biết bài em thích nhất là gì? :)❗Đừng quên Like và Subcribe! Many thanks :xhttps://www.youtube.com/watch?vK5n5l16zYEY&t25s
Đọc tiếp

⚡ Tặng các em playlist nhạc để tập trung khi học bài và cũng thư giãn nữa nhé!
❉ Hãy nghe và comment cho cô biết bài em thích nhất là gì? :)
❗Đừng quên Like và Subcribe! Many thanks :x
https://www.youtube.com/watch?v=K5n5l16zYEY&t=25s
Xem thêm câu trả lời

Chúc mừng các bạn đã đạt giải thưởng thành viên tích cực tháng 5.
Các bạn có tên trong danh sách nhanh chóng gửi cho cô thông tin nhận thưởng nhé.
Dạ, Vâng ạ ;-;
Chúc mừng tất cả mọi người có tên trong đó nha ;-;
Đúng 21
Bình luận (10)
danh sách nào ạ
chúc mừng tất cả mn có trong danh sách nha
Đúng 14
Bình luận (0)
Xem thêm câu trả lời
Chuyên mục VICE, Toán học, số 114. Bài toán dưới đây được tìm thấy tại một đền thờ ở Sabae (Nhật Bản) vào năm 1807. Mọi người hãy thử sức với nhiều cách khác nhau!left{{}begin{matrix}x-y61741y-z14197sqrt[7]{x}+sqrt[7]{y}+sqrt[7]{z}12end{matrix}right.
Đọc tiếp
Chuyên mục VICE, Toán học, số 114. Bài toán dưới đây được tìm thấy tại một đền thờ ở Sabae (Nhật Bản) vào năm 1807. Mọi người hãy thử sức với nhiều cách khác nhau!
\(\left\{{}\begin{matrix}x-y=61741\\y-z=14197\\\sqrt[7]{x}+\sqrt[7]{y}+\sqrt[7]{z}=12\end{matrix}\right.\)
Từ phương trình đã cho suy ra \(\sqrt[7]{z+75938}+\sqrt[7]{z+14197}+\sqrt[7]{z}=12\).
Nếu \(z>2187\Rightarrow VT>12\).
Tương tự với z < 2187.
Suy ra \(z< 2187\) nên y = ...; x = ...
Đúng 11
Bình luận (3)
\(\left\{{}\begin{matrix}x-y=61741\left(1\right)\\y-z=14197\left(2\right)\\\sqrt[7]{x}+\sqrt[7]{y}+\sqrt[7]{z}=12\left(3\right)\end{matrix}\right.\)
Giả sử: x < 0 \(\Rightarrow\) y < 0 \(\Rightarrow\) z < 0 \(\Rightarrow\) \(\sqrt[7]{x}+\sqrt[7]{y}+\sqrt[7]{z}< 0\) \(\Rightarrow\) Vô nghiệm
Với x > 0:
(+) y < 0 \(\Rightarrow\) z < 0 \(\Rightarrow\) Vô nghiệm (x không thỏa mãn (1);(3))
(+) Với y > 0
(-) z < 0 (Vô nghiệm) (CM tương tự)
(-) z > 0 \(\Rightarrow\) x + y + z > 0
Ta có:
\(y-z=14197\Rightarrow y=14197+z\) (1)
\(\left\{{}\begin{matrix}x-y=61741\\y-z=14197\end{matrix}\right.\) \(\Rightarrow\) \(x-z=75938\) \(\Rightarrow\) \(x=75938+z\) (2)
Thay (1), (2) vào \(\sqrt[7]{x}+\sqrt[7]{y}+\sqrt[7]{z}=12\) ta được:
\(\sqrt[7]{75938+z}+\sqrt[7]{14197+z}+\sqrt[7]{z}=12\)
Ta có: Với z > 0 thì \(\sqrt[7]{75938+z}>4,97\)
Vì x, y, z > 0 nên \(\sqrt[7]{x}>4,97\)
Xét x, z là số nguyên:
Với \(\sqrt[7]{x}=5\Rightarrow z=2187\) (z là số nguyên nhỏ nhất có thể tìm được để x nguyên)
Thử lại thấy đúng nên ta tìm được x = 78125; y = 16384; z = 2187
Xét x không là số nguyên:
Với \(\sqrt[7]{x}>5\) \(\Rightarrow\) Không có nghiệm x, y, z thỏa mãn hpt trên
Với \(4,97< \sqrt[7]{x}< 5\) \(\Rightarrow\) Không có nghiệm x, y, z thỏa mãn hpt trên
Vậy x = 78125; y = 16384; z = 2187
Chắc sai :v
Đúng 8
Bình luận (1)
Xem thêm câu trả lời
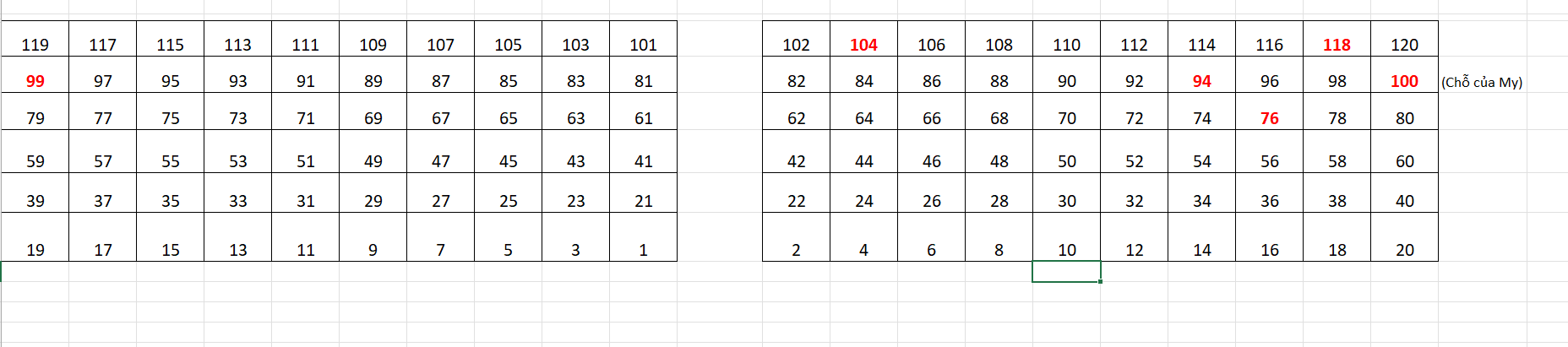
My đi xem phim và đặt ghế số 100. Mỗi hàng ghế bao gồm 20 ghế, 10 ghế mang số chẵn và 10 ghế mang số lẻ như hình dưới đây:Long muốn mua vé để ngồi gần My, nhưng chỉ còn lại các ghế 76, 118, 99, 94, 104. Bạn hay giúp Long chọn vé có ghế gần với My nhất.
Đọc tiếp
My đi xem phim và đặt ghế số 100. Mỗi hàng ghế bao gồm 20 ghế, 10 ghế mang số chẵn và 10 ghế mang số lẻ như hình dưới đây:
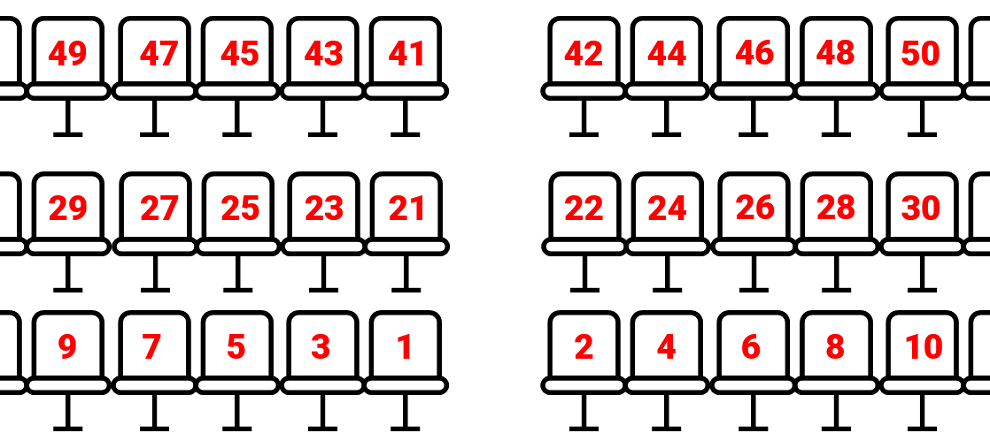
Long muốn mua vé để ngồi gần My, nhưng chỉ còn lại các ghế 76, 118, 99, 94, 104. Bạn hay giúp Long chọn vé có ghế gần với My nhất.
Xem thêm câu trả lời
Tim tất cả các số tự nhiên thỏa mãn tổng của nó với các chữ số cua nó bằng 2004
Lời giải:
Gọi số cần tìm là $A$. Tổng các chữ số của $A$ là $S(A)$.
Vì $A+S(A)=2004$ nên $A$ nhỏ hơn $2004$. Do đó, $A$ nhiều nhất 4 chữ số.
Nếu A có 1 chữ số thì $2A=2004\Rightarrow A=1002$ (vô lý)
Nếu A có 2 chữ số thì $A+S(A)$ lớn nhất bằng $99+9+9=117<2004$ (loại)
Nếu A có 3 chữ số thì $A+S(A)$ lớn nhất bằng $999+9+9+9=1026<2004$ (loại)
Nếu A có 4 chữ số. Gọi $A=\overline{abcd}$.
Ta có: $\overline{abcd}+a+b+c+d=2004$
$\Leftrightarrow 1001a+101b+11c+2d=2004$
$\Rightarrow 1001a\leq 2004\Rightarrow a\leq 2$
Xét các TH sau:
TH1: $a=1$ thì $101b+11c+2d=1003$
$\Rightarrow 101b=1003-11c-2d\geq 1003-11.9-2.9=886$
$\Rightarrow b\geq 9$
$\Rightarrow b=9$.
$11c+2d=94$
$11c=94-2d\geq 94-2.9=76\Rightarrow c\geq 7$
Mà $c$ chẵn nên $c=8$. Kéo theo $d=3$
TH2: $a=2$ thì $101b+11c+2d=2$
$\Rightarrow b=0; c=0; d=1$
Vậy số cần tìm là $1983$ hoặc $2001$
Đúng 7
Bình luận (1)
Lời giải:
Gọi số cần tìm là AA. Tổng các chữ số của AA là S(A)S(A).
Vì A+S(A)=2004A+S(A)=2004 nên AA nhỏ hơn 20042004. Do đó, AA nhiều nhất 4 chữ số.
Nếu A có 1 chữ số thì 2A=2004⇒A=10022A=2004⇒A=1002 (vô lý)
Nếu A có 2 chữ số thì A+S(A)A+S(A) lớn nhất bằng 99+9+9=117<200499+9+9=117<2004 (loại)
Nếu A có 3 chữ số thì A+S(A)A+S(A) lớn nhất bằng 999+9+9+9=1026<2004999+9+9+9=1026<2004 (loại)
Nếu A có 4 chữ số. Gọi A=¯¯¯¯¯¯¯¯¯¯abcdA=abcd¯.
Ta có: ¯¯¯¯¯¯¯¯¯¯abcd+a+b+c+d=2004abcd¯+a+b+c+d=2004
⇔1001a+101b+11c+2d=2004⇔1001a+101b+11c+2d=2004
⇒1001a≤2004⇒a≤2⇒1001a≤2004⇒a≤2
Xét các TH sau:
TH1: a=1a=1 thì 101b+11c+2d=1003101b+11c+2d=1003
⇒101b=1003−11c−2d≥1003−11.9−2.9=886⇒101b=1003−11c−2d≥1003−11.9−2.9=886
⇒b≥9⇒b≥9
⇒b=9⇒b=9.
11c+2d=9411c+2d=94
11c=94−2d≥94−2.9=76⇒c≥711c=94−2d≥94−2.9=76⇒c≥7
Mà cc chẵn nên c=8c=8. Kéo theo d=3d=3
TH2: a=2a=2 thì 101b+11c+2d=2101b+11c+2d=2
⇒b=0;c=0;d=1⇒b=0;c=0;d=1
Vậy số cần tìm là 19831983 hoặc 2001
Đúng 0
Bình luận (0)
Lời giải:
Gọi số cần tìm là AA. Tổng các chữ số của AA là S(A)S(A).
Vì A+S(A)=2004A+S(A)=2004 nên AA nhỏ hơn 20042004. Do đó, AA nhiều nhất 4 chữ số.
Nếu A có 1 chữ số thì 2A=2004⇒A=10022A=2004⇒A=1002 (vô lý)
Nếu A có 2 chữ số thì A+S(A)A+S(A) lớn nhất bằng 99+9+9=117<200499+9+9=117<2004 (loại)
Nếu A có 3 chữ số thì A+S(A)A+S(A) lớn nhất bằng 999+9+9+9=1026<2004999+9+9+9=1026<2004 (loại)
Nếu A có 4 chữ số. Gọi A=¯¯¯¯¯¯¯¯¯¯abcdA=abcd¯.
Ta có: ¯¯¯¯¯¯¯¯¯¯abcd+a+b+c+d=2004abcd¯+a+b+c+d=2004
⇔1001a+101b+11c+2d=2004⇔1001a+101b+11c+2d=2004
⇒1001a≤2004⇒a≤2⇒1001a≤2004⇒a≤2
Xét các TH sau:
TH1: a=1a=1 thì 101b+11c+2d=1003101b+11c+2d=1003
⇒101b=1003−11c−2d≥1003−11.9−2.9=886⇒101b=1003−11c−2d≥1003−11.9−2.9=886
⇒b≥9⇒b≥9
⇒b=9⇒b=9.
11c+2d=9411c+2d=94
11c=94−2d≥94−2.9=76⇒c≥711c=94−2d≥94−2.9=76⇒c≥7
Mà cc chẵn nên c=8c=8. Kéo theo d=3d=3
TH2: a=2a=2 thì 101b+11c+2d=2101b+11c+2d=2
⇒b=0;c=0;d=1⇒b=0;c=0;d=1
Vậy số cần tìm là 19831983 hoặc 20012001
Đúng 0
Bình luận (0)
[Lớp 7]Bài 1. Điểm kiểm tra môn Toán của tất cả học sinh trong lớp 7A được cho trong bảng sau Điểm (x)345678910 Tần số (n) 1 a 3 7 7 9 8 3N40a) Tìm a.b) Tìm số trung bình cộng của dấu hiệu. Tìm mốt của dấu hiệu.Bài 2.Cho đơn thức Pleft(-3x^3y^2right)^2.xy^3.a) Thu gọn P, cho biết phần hệ số, phần biến và bậc của đơn thức P.b) Tính giá trị của đơn thức P tại x1; y-1.Bài 3.Cho hai đa thức Aleft(xright)-3x^2-2x^4-2+7x và Bleft(xright)3x^2+4x-5+2x^4.a) Hãy sắp xếp các hạng tử của mỗ...
Đọc tiếp

[Lớp 7]
Bài 1. Điểm kiểm tra môn Toán của tất cả học sinh trong lớp 7A được cho trong bảng sau
| Điểm (x) | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|
| Tần số (n) | 1 | a | 3 | 7 | 7 | 9 | 8 | 3 | N=40 |
a) Tìm \(a\).
b) Tìm số trung bình cộng của dấu hiệu. Tìm mốt của dấu hiệu.
Bài 2.
Cho đơn thức \(P=\left(-3x^3y^2\right)^2.xy^3.\)
a) Thu gọn \(P\), cho biết phần hệ số, phần biến và bậc của đơn thức \(P\).
b) Tính giá trị của đơn thức \(P\) tại x=1; y=-1.
Bài 3.
Cho hai đa thức \(A\left(x\right)=-3x^2-2x^4-2+7x\) và \(B\left(x\right)=3x^2+4x-5+2x^4.\)
a) Hãy sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến.
b) Tính \(M\left(x\right)=A\left(x\right)+B\left(x\right).\) Tìm \(x\) để \(M\left(x\right)=4\).
c) Tìm đa thức \(C\left(x\right)\) sao cho \(C\left(x\right)-B\left(x\right)=-A\left(x\right).\)
Bài 4.
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Chứng minh hai tam giác ABH, ACH bằng nhau.
b) Cho AB=10 cm, BC=12 cm, tính AH.
c) Kẻ HE song song với AC, E thuộc AB. Chứng minh tam giác AEH cân.
d) Gọi F là trung điểm của AH. Chứng minh \(BF+HE>\dfrac{3}{4}BC.\)
Bài 5.
Cho đa thức \(f\left(x\right)=ax^2+bx+c\) với \(a,b,c\) là các số hữu tỉ không âm. Biết \(a+3c=2019\) và \(a+2b=2020.\) Chứng minh rằng \(f\left(1\right)\le2019\dfrac{1}{2}.\)
Bài 4:
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔBAC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
Đúng 2
Bình luận (0)
Bài 1. Điểm kiểm tra môn Toán của tất cả học sinh trong lớp 7A được cho trong bảng sau
Điểm (x) | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
Tần số (n) | 1 | a | 3 | 7 | 7 | 9 | 8 | 3 | N=40 |
a) Tìm a
b) Tìm số trung bình cộng của dấu hiệu. Tìm mốt của dấu hiệu.
a) a= 40-(1+3+7+7+9+8+3)=2
vậy a=2
b) X=![]() =7.3
=7.3
Mo=8
Đúng 3
Bình luận (0)
Xem thêm câu trả lời