Con lắc đơn

bạn để ý có công thức T= \(mg\left(3cos\alpha-2cos\alpha_0\right)\)

còn P= mg

vậy T/P= \(3cos\alpha-2cos\alpha_0\)

a₀* l = S₀    bạn suy ra a₀   (  l: chiều dài con lắc ;  w² = g/l)

chú ý: con lắc qua vị trí cân bằng tức \(\alpha=0\)  suy ra cos \(\alpha\) = 1

suy ra T/P cần tìm =  3 - 2cos\(\alpha_0\)         

bạn hiểu rồi thì tính nốt nhé

giảm chiều dài 0,1%

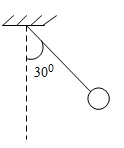
a) \(v=\sqrt{2gl\left(1-\cos\alpha\right)}\)
b) Tại vị trí này, toàn bộ thế năng ban đầu của con lắc đã chuyển hóa thành động năng, còn ở các vị trí khác chỉ một phần thế năng ban đầu chuyển hóa thành động năng. Do đó, vận tốc tại vị trí này là cực đại.

Chu kỳ dao động của con lắc đơn là
\(T=2\pi\sqrt{\frac{l}{g}}\)

\(l=g\left(\frac{T}{2\pi}\right)^2\)

\(l\) tỉ lệ với \(T^2\)

suy ra 

\(T^2=T^2_1+T^2_2\)

T=2,5s 

\(\rightarrow A\)

CLĐ là cái chi bạn ?

Câu trả lời  click vào đây bạn nhé 

Đây là một bài tương tự đã được trả lời rùi.

Gia tốc trong dao động của con lắc đơn gồm 2 thành phần: tiếp tuyến + hướng tâm.

Giả sử biên độ góc là \(\alpha_0\), để tìm gia tốc khi biên độ góc là \(\alpha\le\alpha_0\) ta làm như sau:

+ Gia tốc hướng tâm: \(a_{ht}=\frac{v^2}{l}=\frac{2gl\left(\cos\alpha-\cos\alpha_0\right)}{l}=2g\left(\cos\alpha-\cos\alpha_0\right)\)

+ Gia tốc tiếp tuyến: \(a_{tt}=\frac{F_{tt}}{m}=g\sin\alpha\)

+ Gia tốc là a \(\Rightarrow a^2=a_{ht}^2+a_{tt}^2=g\left[4\left(\cos\alpha-\cos\alpha_0\right)^2+\sin^2\alpha\right]\)\(=g\left[3\cos^2\alpha-8\cos\alpha_0\cos\alpha+1\right]\)

Suy ra a min khi \(\cos\alpha=\frac{4}{3}\cos\alpha_0\) 

Khi đó, lực căng dây là: \(\tau=mg\left(3\cos\alpha-2\cos\alpha_0\right)=2mg\cos\alpha_0\)

Tỉ số lực căng dây: \(\frac{\tau_2}{\tau_1}=\frac{\cos\alpha_2}{\cos\alpha_1}=\frac{\cos60^0}{\cos30^0}=0,58\)

Khi nói đại lượng Y có phụ thuộc vào X hay không thì X không phải là đại lượng dẫn xuất (là đại lượng có thể đc biểu diễn theo thuộc tính khác)

Ở đây, bình phương tốc độ góc đã biểu diễn theo g và l: \(\omega^2=\frac{g}{l}\)nên chưa thể kết luận đc.

\(\dfrac{F_{đhmax}}{F_{đhmin}}=\dfrac{k(\Delta l_0+A)}{k(\Delta l_0-A)}=3,5\)

\(\Rightarrow A=\dfrac{5}{9}\Delta l_0\)

Biên độ tăng 1,5 lần thì \(A'=1,5A=\dfrac{2,5}{3}\Delta l_0\)

Khi đó, tỉ số đàn hồi sẽ là: \(\dfrac{F_{đhmax}}{F_{đhmin}}=\dfrac{k(\Delta l_0+A)}{k(\Delta l_0-A)}=\dfrac{k(\Delta l_0+\dfrac{2,5}{3}\Delta l_0)}{k(\Delta l_0-\dfrac{2,5}{3}\Delta l_0)}=11\)