Question

ý c,d là đúng hay sai vậy mn

 

Answer 1

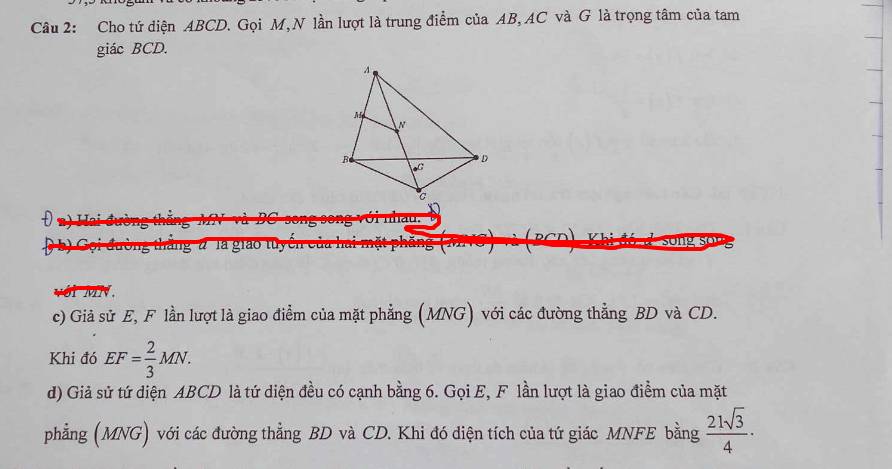
a: Xét ΔABC có

M,N lần lượt là trung điểm của AB,AC

=>MN là đường trung bình của ΔABC

=>MN//BC

=>Đúng

b: Xét (MNG) và (BCD) có

G∈(MNG) giao (BCD)

MN//BC

Do đó: (MNG) giao (BCD)=xy, xy đi qua G và xy//MN//BC

=>Đúng

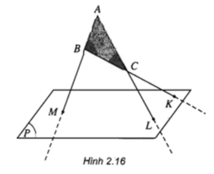
c: Chọn mp(BCD) có chứa BD và CD

(BCD) giao (MNG)=xy

xy//BC

Do đó: EF//BC

Gọi K là trung điểm của BC

Xét ΔDBC có

G là trọng tâm

K là trung điểm của BC

Do đó: D,G,K thẳng hàng

=>\(DG=\frac23DK\)

Xét ΔDBK có EG//BK

nên \(\frac{DG}{DK}=\frac{DE}{DB}\)

=>\(\frac{DE}{DB}=\frac23\)

Xét ΔDBC có EF//BC

nên \(\frac{EF}{BC}=\frac{DE}{DB}=\frac23\)

=>\(EF=\frac23BC\)

=>\(\frac{EF}{MN}=\frac23:\frac12=\frac43\)

=>Sai