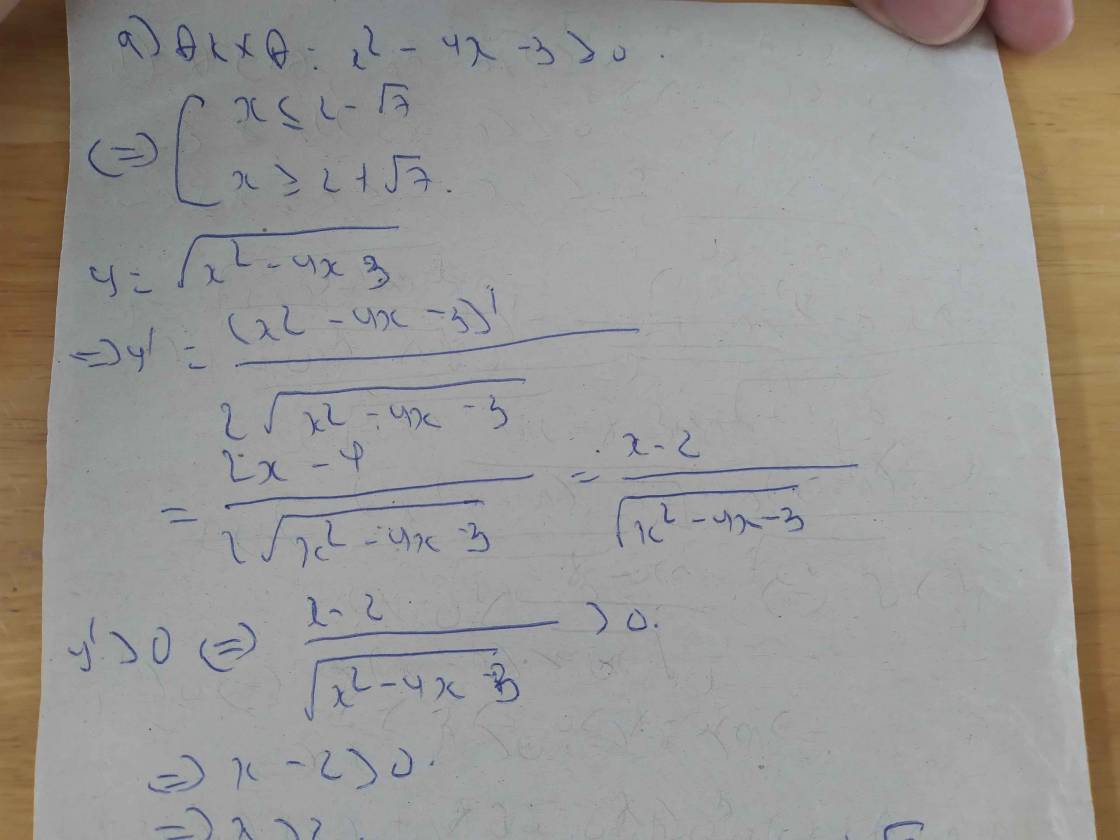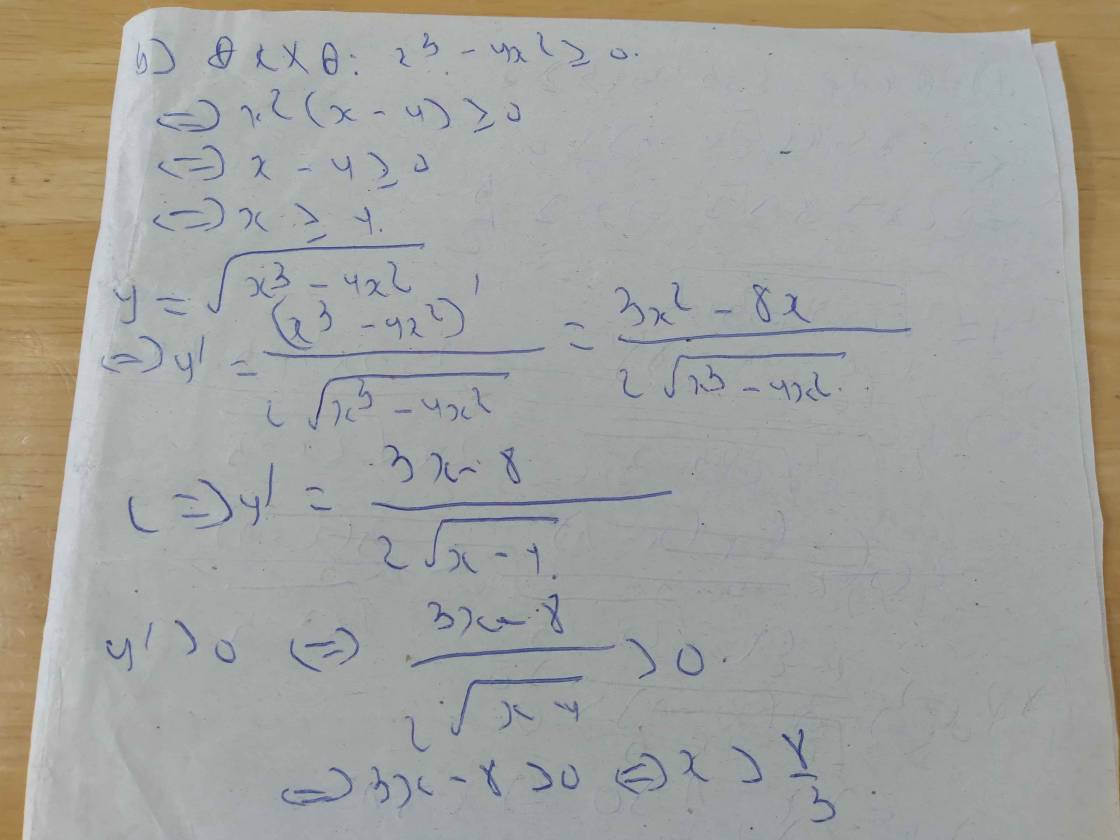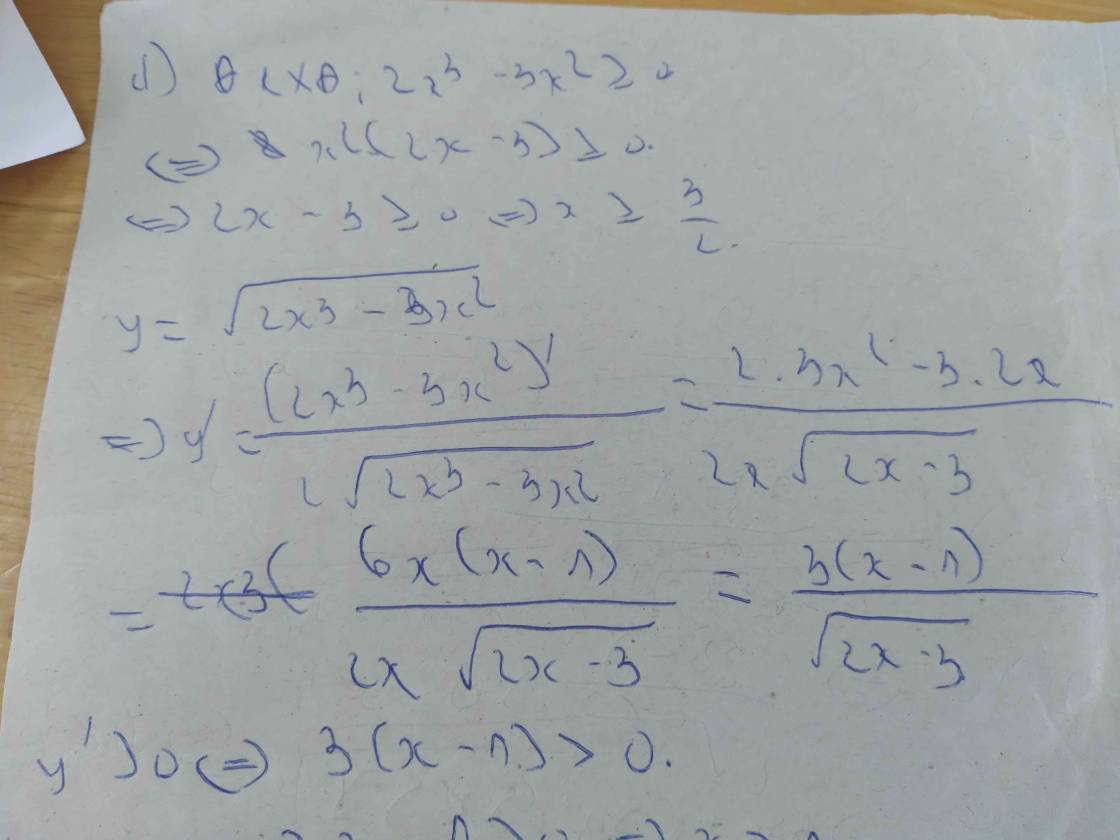Các câu hỏi tương tự
a) Giải phương trình trên tập số thực:
\(x^3-4x^2-5x+6=\sqrt[3]{7x^2+9x-4}\)
b) Giải hệ phương trình sau:
\(\left\{{}\begin{matrix}x^2+2x\sqrt{xy}=y^2\sqrt{y}\\\left(4x^3+y^3+3x^2\sqrt{x}\right)\left(15\sqrt{x}+y\right)=3\sqrt{x}\left(y\sqrt{y}+x\sqrt{y}+4x\sqrt{x}\right)^2\end{matrix}\right.\) ; với \(x,y\inℝ\)
tìm khoảng đồng biến nghịch biến
a) \(y=\left(x^2-1\right)^2\)
b) \(y=\left(3x+4\right)^3\)
c) \(y=\left(x+3\right)^2\left(x-1\right)\)
d) \(y=\left(2x+2\right)\left(x^3-1\right)\)
xét tính đồng biến nghịch biến
a) \(y=\sqrt{3x^3-x^2-x}\)
b) \(y=\sqrt{x^2-x-1}\)
c) \(y=\sqrt{x^2-2x}\)
d) \(y=\sqrt{3x^2-2x+1}\)
tìm khoảng đồng biến nghịch biến
a) \(y=\left(x+2\right)^2\)
b) \(y=\left(x^2-1\right)\left(x+2\right)\)
c) \(y=\left(x+2\right)\left(2x^2-3\right)\)
d) \(y=\left(x-1\right)^2\left(x+2\right)\)
tìm khoảng đồng biến và nghịch biến của hàm số sau
a) \(y'=\left(x-3\right)^3\left(x-1\right)^{22}\left(-3x-6\right)^7\)
b) \(y'=\left(4x-3\right)^3\left(x^2-1\right)^{21}\left(3x-9\right)^7\)
tìm khoảng đồng biến nghịch biến
a) \(y=\left(5x-10\right)^4\)
b) \(y=\left(-x-1\right)\left(x+2\right)^4\)
c) \(y=\left(x^3-1\right)^3\)
d) \(y=\left(x^2-1\right)\left(x+2\right)\)
tìm khoảng đồng biến nghịch biến
a) \(y=\sqrt{4x-x^2}\)
b) \(y=\sqrt{16-x^2}\)
c) \(y=\dfrac{x^2-2x+2}{x^2+3}\)
tìm khoảng đồng biến nghịch biến
a) \(y=\sqrt{x^2+2x+3}\)
b) \(y=\sqrt{4-x^2}\)
c) \(y=\dfrac{x^2-6x+10}{x-3}\)
d) \(y=\sqrt{-x+2x}\)
e) \(y=\sqrt{4+5x^2}\)
tính đạo hàm
a) \(y=\sqrt{\left(x+2\right)\left(x+3\right)}\)
b) \(y=\sqrt{\dfrac{2x+1}{x-3}}\)
c) \(y=\left(x+1\right)\sqrt{x+3}\) tính y'(1)
d) \(y=\dfrac{x-1}{x^2+1}\)