Các câu hỏi tương tự
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số:
y
x
2
-
6
x
+
9
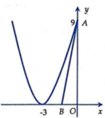
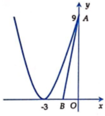
và 2 đường thẳng x 0; y 0 Đường thẳng (d) có hệ số k và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 - 6 x + 9 và 2 đường thẳng x = 0; y = 0 Đường thẳng (d) có hệ số k và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
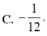
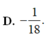
Gọi (H) là hình phẳng giới hạn bởi parabol (P)
y
8
x
-
x
2
và trục hoành. Các đường thẳng y a; y b;y c với 0abc16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức
16
-
a
3
+
16
-
b...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi parabol (P) y = 8 x - x 2 và trục hoành. Các đường thẳng y = a; y = b;y =c với 0<a<b<c<16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức 16 - a 3 + 16 - b 3 + 16 - c 3 bằng
A. 2048.
B. 3584.
C. 2816.
D. 3480.
Cho hình thang cong (H) giới hạn bởi các đường
y
3
x
,
y
0
,
x
0
,
x
2
. Đường thẳng xt (0t2) chia (H) thành hai phần có diện tích S1 và S2 (như hình vẽ). Tìm t để S13 S2
Đọc tiếp
Cho hình thang cong (H) giới hạn bởi các đường y = 3 x , y = 0 , x = 0 , x = 2 . Đường thẳng x=t (0<t<2) chia (H) thành hai phần có diện tích S1 và S2 (như hình vẽ). Tìm t để S1=3 S2
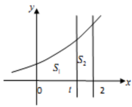
Cho hình thang cong (H) giới hạn bởi các đường
y
3
x
, y0, x0, x2. Đường thẳng xt chia H thành hai phần có diện tích
S
1
và
S
2
(như hình vẽ). Tìm t để
S
1
3
S
2
Đọc tiếp
Cho hình thang cong (H) giới hạn bởi các đường y = 3 x , y=0, x=0, x=2. Đường thẳng x=t chia H thành hai phần có diện tích S 1 và S 2 (như hình vẽ). Tìm t để S 1 = 3 S 2
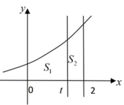
Xét hình phẳng (H) được giới hạn bởi hàm số
y
x
2
, đường thẳng
y
k
2
với
0
≤
k
≤
1
; trục tung và đường thẳng x1. Biết (H) được chia thành hai phần có diện tích
S
1
S
2
như hình vẽ. Gọi...
Đọc tiếp
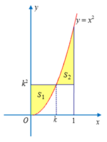
Xét hình phẳng (H) được giới hạn bởi hàm số y = x 2 , đường thẳng y = k 2 với 0 ≤ k ≤ 1 ; trục tung và đường thẳng x=1. Biết (H) được chia thành hai phần có diện tích S 1 S 2 như hình vẽ. Gọi k 1 , k 2 lần lượt là giá trị của k làm cho tổng S 1 + S 2 có giá trị lớn nhất và nhỏ nhất. Tính giá trị của T = k 1 + k 2
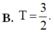
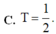
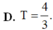
Cho hàm số
y
a
x
4
+
b
x
2
+
c
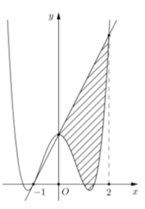
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0; x2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x = 0 có diện tích bằng:
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Diện tích hình phẳng giới hạn bởi các đường thẳng y 1, y x và đồ thị hàm số
y
x
2
4
trong miền
x
≥
0
,
y
≤
1
là a/b. Khi đó b - a bằng A. 4 B. 2 C. 3 D. 1
Đọc tiếp
Diện tích hình phẳng giới hạn bởi các đường thẳng y = 1, y = x và đồ thị hàm số y = x 2 4 trong miền x ≥ 0 , y ≤ 1 là a/b. Khi đó b - a bằng
A. 4
B. 2
C. 3
D. 1
Một hình phẳng được giới hạn bởi y
e
-
x
, y 0, x 0, x 1. Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên).a) Tính diện tích Sn của hình bậc thang (tổng diện tích của n hình chữ nhật con).b) Tìm và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.
Đọc tiếp
Một hình phẳng được giới hạn bởi y = e - x , y = 0, x = 0, x = 1. Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên).
a) Tính diện tích Sn của hình bậc thang (tổng diện tích của n hình chữ nhật con).
b) Tìm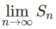 
và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.
Cho hàm số
y
a
x
4
+
b
x
2
+
c
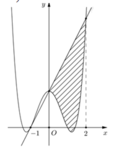
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của A cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x0; x2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ).Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳn...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của A cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ).Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x = 0; x=2 có diện tích bằng
A. 2/5
B. 1/9
C. 2/9
D. 1/5