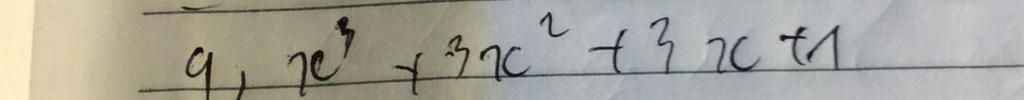Question

 

Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu

Answer 1

HĐT số 4: \(\left(A+B\right)^3=A^3+3A^2B+3AB^2+B^3\)

__________

\(x^3+3x^2+3x+1\)

\(=x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3\)

\(=\left(x+1\right)^3\)

Answer 2

`x^3 +3x^2+3x+1`

`= x^3 + 3*x^2*1 +3*x*1^2 +1^3`

`=(x+1)^3`

Answer 3

x^3 + 3x^2 + 3x + 1

<=> x^3 + 3x^2.1 + 3x.1^2 + 1^3

<=> (x + 1) ^3