a: Xét (O) có
PE,PF là các tiếp tuyến
Do đó: PE=PF
=>P nằm trên đường trung trực của EF(1)
Ta có: OE=OF
=>O nằm trên đường trung trực của EF(2)
Từ (1),(2) suy ra PO là đường trung trực của EF
=>PO⊥EF tại N và N là trung điểm của FE
Xét ΔEBF có
I,N lần lượt là trung điểm của EH,EF
=>IN là đường trung bình của ΔEBF
=>IN//HF
b: IN//HF
=>\(\hat{ENI}=\hat{EFH}=\hat{EFB}\) (hai góc đồng vị)(1)
Xét (O) có
\(\hat{EFB};\hat{EMB}\) là các góc nội tiếp chắn cung EB
=>\(\hat{EFB}=\hat{EMB}\left(2\right)\)
Từ (1),(2) suy ra \(\hat{EMI}=\hat{ENI}\)
=>EMNI là tứ giác nội tiếp
Ta có: IN//HF
HF⊥HE
Do đó: IN⊥HE tại I
Ta có: EMNI là tứ giác nội tiếp
=>\(\hat{EIN}+\hat{EMN}=180^0\)
=>\(\hat{EMN}=180^0-90^0=90^0\)
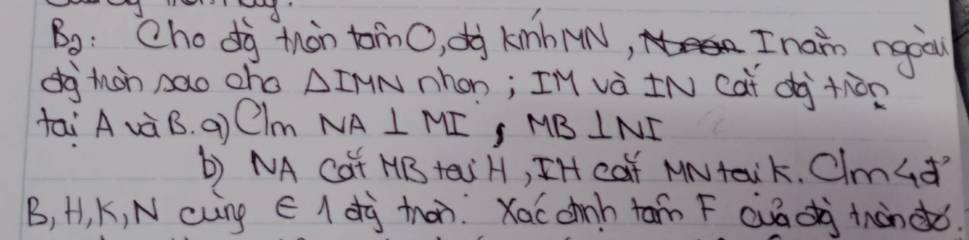
vẽ hình luôn ạ
