1: Xét tứ giác AKHB có \(\hat{AKB}=\hat{AHB}=90^0\)
nên AKHB là tứ giác nội tiếp đường tròn đường kính AB
=>A,K,H,B cùng thuộc đường tròn đường kính AB(1)
Xét tứ giác AIHB có \(\hat{AIB}=\hat{AHB}=90^0\)
nên AIHB là tứ giác nội tiếp đường tròn đường kính AB
=>A,I,H,B cùng thuộc đường tròn đường kính AB(2)
Từ (1),(2) suy ra A,K,H,I,B cùng thuộc đường tròn đường kính AB
=>AIKH là tứ giác nội tiếp
Ta có: ABHK nội tiếp
=>\(\hat{AHK}=\hat{ABK}\) (3)
Xét (O) có
\(\hat{BAD};\hat{BCD}\) là các góc nội tiếp chắn cung BD
=>\(\hat{BAD}=\hat{BCD}\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
ta có: \(\hat{ABK}+\hat{BAD}=90^0\) (ΔAKB vuông tại K)
\(\hat{BCD}+\hat{ACB}=\hat{ACD}=90^0\)
mà \(\hat{BAD}=\hat{BCD}\)
nên \(\hat{ABK}=\hat{ACB}\) (4)
Từ (3),(4) suy ra \(\hat{AHK}=\hat{ACB}\)
Ta có: \(\hat{KHC}+\hat{KHA}=\hat{AHC}=90^0\)
\(\hat{CBI}+\hat{ICB}=90^0\) (ΔCBI vuông tại I)
mà \(\hat{KHA}=\hat{ICB}\left(\hat{AHK}=\hat{ACB}\right)\)
nên \(\hat{KHC}=\hat{CBI}=\hat{IBC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên HK//BI
=>HK⊥AC
2: Trên cạnh AC, lấy E sao cho \(\hat{ABE}=\hat{CBD}\)
=>\(\hat{ABD}+\hat{EBD}=\hat{CBE}+\hat{EBD}\)
=>\(\hat{ABD}=\hat{CBE}\)
mà \(\hat{ABD}=\hat{ACD}\)
nên \(\hat{CBE}=\hat{ACD}\)
Xét ΔECB và ΔADB có
\(\hat{CBE}=\hat{ABD}\)
\(\hat{ECB}=\hat{ADB}\)
Do đó: ΔECB~ΔADB
=>\(\frac{EB}{AB}=\frac{CB}{DB}=\frac{EC}{AD}\)
=>\(AD\cdot BC=EC\cdot DB\)
Xét ΔABE và ΔDBC có
\(\hat{ABE}=\hat{DBC}\)
\(\hat{BAE}=\hat{BDC}\)
Do đó: ΔABE~ΔDBC
=>\(\frac{AE}{DC}=\frac{AB}{DB}\)
=>\(AB\cdot DC=DB\cdot AE\)
\(AD\cdot BC+AB\cdot DC=EC\cdot DB+AE\cdot DB=DB\left(EC+AE\right)=DB\cdot AC\)

















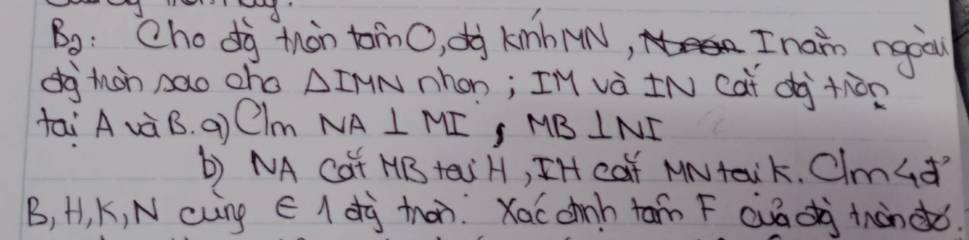

 vẽ hình luôn ạ
vẽ hình luôn ạ
