Đáp án A
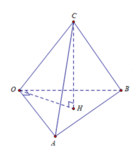
Gọi H là hình chiếu của C lên (OAB)
Khi đó: C O H ^ = O C ; O A B ^
Ta có: C H = 3 V S O A B = 3. 1 12 1 2 .1.1 = 1 2
sin C O H ^ = C H C O = 1 2 1 = 1 2 ⇒ C O H ^ = 30 °

Đáp án A
Gọi H là hình chiếu của C lên (OAB)
Khi đó: C O H ^ = O C ; O A B ^
Ta có: C H = 3 V S O A B = 3. 1 12 1 2 .1.1 = 1 2
sin C O H ^ = C H C O = 1 2 1 = 1 2 ⇒ C O H ^ = 30 °
Cho tứ diện OABC có các góc tại đỉnh O đều bằng 90 ° và O A = a , O B = b ; O C = c . Gọi G là trọng tâm của tứ diện. Thể tích của khối tứ diện GABC bằng
A. a b c 6
B. a b c 8
C. a b c 4
D. a b c 24
Tứ diện OABC có OA = OB = OC = 1 và O A ⊥ O B . Tìm góc giữa OC và (OAB) để tứ diện có thể tích là 1 12
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và O A = a , O B = b , O C = c . Thể tích tứ diện OABC là
A. V = a b c 12
B. V = a b c 4
C. V = a b c 3
D. V = a b c 6
Cho tứ diện OABC có OA,OB,OC đội một vuông góc, O A = a , O B = b , O C = c . Tính khoảng cách d từ O tới mặt phẳng (ABC).
A. d = a b c a 2 b 2 + b 2 c 2 + c 2 a 2
B. d = a 2 + b 2 + c 2 3
C. d = a b + b c + c a a 2 + b 2 + c 2
D. d = a 2 b 2 c 2 a 2 b 2 + b 2 c 2 + c 2 a 2
Cho tứ diện OABC có OA;OB;OC đôi một vuông góc và O A = a , O B = b , O C = c . Tính thể tích khối tứ diện OABC.
A. abc
B. abc/3
C. abc/6
D. abc/2
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và OA=a,OB=b,OC=c Tính thể tích khói tứ diện OABC
A. a b c 3 .
B. a b c 4 .
C. a b c 6 .
D. a b c 2 .
Trong không gian cho ba tia Ox,Oy,Oz đôi một vuông góc và các điểm A,B,C không trùng với O lần lượt thay đổi trên các tia Ox,Oy,Oz và luôn thoả mãn điều kiện: tỉ số giữa diện tích tam giác ABC và thể tích khối tứ diện OABC bằng 3 2 . Khối diện OABC có thể tích nhỏ nhất bằng
A. 6
B. 3 2
C. 4 3
D. 27 3 2
Cho tứ diện OABC có ba cạnh OA;OB;OC đôi một vuông góc với nhau, O A = a 2 2 , O B = O C = a . Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC)Tính thể tích khối tứ diện OABH
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Tứ diện OABC, có OA=a, OB=b, OC=c và đôi một vuông góc với nhau. Thể tích khối tứ diện bằng
A. a b c 3
B. abc
C. a b c 6
D. a b c 2