Question

Cho tứ diện OABC có OA,OB,OC đội một vuông góc, O A = a , O B = b , O C = c . Tính khoảng cách d từ O tới mặt phẳng (ABC).

A. d = a b c a 2 b 2 + b 2 c 2 + c 2 a 2

B. d = a 2 + b 2 + c 2 3

C. d = a b + b c + c a a 2 + b 2 + c 2

D.  d = a 2 b 2 c 2 a 2 b 2 + b 2 c 2 + c 2 a 2

Answer 1

Đáp án A

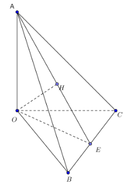
Gọi H là hình chiếu của O lên mặt phẳng (ABC) nên O H ⊥ A B C ⇒ O H ⊥ B C 1 .

Mặt khác O A ⊥ O B , O A ⊥ O C ⇒ O A ⊥ O B C ⇒ O A ⊥ B C 2 .

Từ (1),(2) suy ra B C ⊥ A O H ⇒ B C ⊥ A H . Chứng minh tương tự ta được A B ⊥ C H . Suy ra H là trực tâm của ΔABC.

Trong mặt phẳng (ABC) gọi E là giao điểm của AH và BC.

Ta có O H ⊥ A B C ⇒ O H ⊥ A E  tại H.

O A ⊥ A B C ⇒ O A ⊥ O E  tức là OH là đường cao của tam giác vuông OAE.

Mặt khác OE là đường cao của tam giác vuông OBC.

Do đó: 1 O H 2 = 1 O A 2 + 1 O E 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 .

⇔ 1 d 2 = 1 a 2 + 1 b 2 + 1 c 2 ⇒ d = a b c b 2 c 2 + a 2 c 2 + a 2 b 2 .