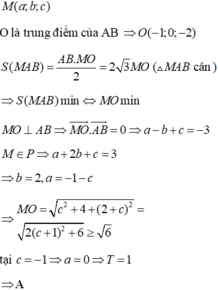Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng
P
:
x
+
y
-
z
+
2
0
và hai điểm
A
7
;
-
4
;
-
3
,
B
3
;
4
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng P : x + y - z + 2 = 0 và hai điểm A 7 ; - 4 ; - 3 , B 3 ; 4 ; 1 . Gọi M a ; b ; c là điểm thuộc P a < 2 sao cho tam giác AMB vuông tại M và có diện tích nhỏ nhất. Giá trị của biểu thức 3 a + 9 b + 63 c bằng
A. 140
B. -38
C. 154
D. -21
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(3;1;2), M(3;0;0) và mặt phẳng (P):x+y+z-30. Đường thẳng
∆
đi qua điểm M, nằm trong mặt phẳng (P) sao cho khoảng cách từ điểm A đến đường thẳng
∆
là nhỏ nhất. Gọi
u
→
a
,
b
,
c
là vectơ chỉ phương của
∆
với a, b, c là các số nguyên có ước...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(3;1;2), M(3;0;0) và mặt phẳng (P):x+y+z-3=0. Đường thẳng ∆ đi qua điểm M, nằm trong mặt phẳng (P) sao cho khoảng cách từ điểm A đến đường thẳng ∆ là nhỏ nhất. Gọi u → = a , b , c là vectơ chỉ phương của ∆ với a, b, c là các số nguyên có ước chung lớn nhất bằng 1. Tính giá trị T=a+b+c.
A. T = -1
B. T = 1.
C. T = 0.
D. T = 2.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
-
1
2
+
y
-
2
2
+
z
-
3
2
16
và các điểm A(1;0;2), B(-1;2;2)....
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x - 1 2 + y - 2 2 + z - 3 2 = 16 và các điểm A(1;0;2), B(-1;2;2). Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) và mặt cầu (S ) có diện tích nhỏ nhất. Khi đó viết phương trình (P):ax + by + cz + 3 = 0. Tính giá trị của T = a + b + c.
A. 3
B. -3
C. 0
D. -2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
−
1
2
+
y
−
2
2
+
z
−
3
2
16
và các điểm
A...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 1 2 + y − 2 2 + z − 3 2 = 16 và các điểm A 1 ; 0 ; 2 , B − 1 ; 2 ; 2 . Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) với mặt cầu (S) có diện tích nhỏ nhất. Khi viết phương trình (P) dưới dạng ax+by+cz+3=0. Tính tổng T=a+b+c
A. 3
B. -3
C. 0
D. -2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
-
1
2
+
y
-
2
2
+
z
-
3
2
16
và các điểm A(1;0;2), B(-1;2;2)....
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x - 1 2 + y - 2 2 + z - 3 2 = 16 và các điểm A(1;0;2), B(-1;2;2). Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) với mặt cầu (S) có diện tích nhỏ nhất. Khi viết phương trình (P) dưới dạng ax+by+cz+3=0. Tính tổng T=a+b+c
A. 3
B. -3
C. 0
D. -2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
−
1
2
+
y
−
2
2
+
z
−
3
2
16...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 1 2 + y − 2 2 + z − 3 2 = 16 và các điểm A 1 ; 0 ; 2 , B − 1 ; 2 ; 2 . Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) với mặt cầu (S) có diện tích nhỏ nhất. Khi viết phương trình (P) dưới dạng a x + b y + c z + 3 = 0. Tính tổng T = a + b + c
A. 3
B. -3
C. 0
D. -2
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P):x-y+z-40 và hai điểm A(-2;2;4),B(2;6;6). Gọi M là điểm di động trên (P) sao cho tam giác MAB vuông tại M. Gọi a,b lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của độ dài OM. Giá trị của biểu thức
a
2
+
b
2
bằng A.
4
61
B. 104. C. 122. D.
4
52
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P):x-y+z-4=0 và hai điểm A(-2;2;4),B(2;6;6). Gọi M là điểm di động trên (P) sao cho tam giác MAB vuông tại M. Gọi a,b lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của độ dài OM. Giá trị của biểu thức a 2 + b 2 bằng
A. 4 61
B. 104.
C. 122.
D. 4 52
Trong không gian với hệ tọa độ Oxyz, biết M(a,b,c) (với a 0) là điểm thuộc đường thẳng
Δ
:
x
1
y
+
2
−
1
z
−
1
2
và cách mặt phẳng
P
:
2
x
−
y
+
2
z
−
5
0
một khoảng bằng 2. Tính g...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, biết M(a,b,c) (với a > 0) là điểm thuộc đường thẳng Δ : x 1 = y + 2 − 1 = z − 1 2 và cách mặt phẳng P : 2 x − y + 2 z − 5 = 0 một khoảng bằng 2. Tính giá trị của T=a+b+c
A. T = -1
B. T = -3
C. T = 3.
D. T = 1.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
P
:
x
+
y
+
z
-
1
0
và hai điểm A ( 1;-3;0 ), B ( 5;-1;-2 ). Điểm m ( a;b;c ) trên mặt phẳng (P) sao cho
M
A
-
M
B
đạt giá trị lớn nhất. Tính tổng a + b + c A. 1 B. 11 C. 5 D. 6
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x + y + z - 1 = 0 và hai điểm A ( 1;-3;0 ), B ( 5;-1;-2 ). Điểm m ( a;b;c ) trên mặt phẳng (P) sao cho M A - M B đạt giá trị lớn nhất. Tính tổng a + b + c
A. 1
B. 11
C. 5
D. 6