v = (5; -3; 1)
⇒ 2v = (10; -6; 2)
⇒ 2v - u = (10; -6; 2) - (3; -1; -2)
= (10 - 3; -6 + 1; 2 + 2)
= (7; -5; 4)
v = (5; -3; 1)
⇒ 2v = (10; -6; 2)
⇒ 2v - u = (10; -6; 2) - (3; -1; -2)
= (10 - 3; -6 + 1; 2 + 2)
= (7; -5; 4)
Trong không gian với hệ tọa độ Oxyz, cho hai véctơ
a
→
=(2;-3;1) và ![]() =(-1;0;4). Tìm tọa độ véctơ
u
→
=-2
a
→
+3
=(-1;0;4). Tìm tọa độ véctơ
u
→
=-2
a
→
+3![]() .
.
A.![]() =(-7;6;-10)
=(-7;6;-10)
B.![]() =(-7;6;10)
=(-7;6;10)
C.![]() =(7;6;10)
=(7;6;10)
D.![]() =(-7;-6;10)
=(-7;-6;10)
Trong không gian với hệ tọa độ Oxyz cho hai véctơ a → = ( 2 ; - 3 ; 1 ) và b → = ( - 1 ; 0 ; 4 ) Tìm tọa độ véctơ u → = - 2 a → + 3 b →
A. u → = ( - 7 ; 6 ; - 10 )
B. u → = ( - 7 ; 6 ; 10 )
C. u → = ( 7 ; 6 ; 10 )
D. u → = ( - 7 ; - 6 ; 10 )
Trong không gian với hệ trục tọa độ Oxyz, cho hai véctơ u → = 2 ; 3 ; - 1 và v → = 5 ; - 4 ; m . Tìm m để u → ⊥ v →
A. - 2
B. 2
C. 4
D. 0
Trong không gian hệ tọa độ Oxyz, cho u → = ( 1 ; 2 ; - 1 ) và v → = ( 2 ; 1 ; 0 ) . Tính [ u → , v → ] .
![]()
![]()
![]()
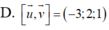
Trong không gian với hệ tọa độ Oxyz, cho vecto u → = ( x ; 2 ; 1 ) và vec tơ v → = ( 1 ; - 1 ; 2 x ) . Tính tích vô hướng của u → v à v → .
A. -2 - x
B. 3x + 2
C. 3x - 2
D. x + 2
Trong không gian hệ tọa độ Oxyz, mặt cầu (S) có tâm I(3;-3;1) và đi qua điểm A(5;-2;1) có phương trình là
A. ( x - 5 ) 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 5
B. ( x - 3 ) 2 + ( y + 3 ) 2 + ( z - 1 ) 2 = 25
C. ( x + 3 ) 2 + ( y - 3 ) 2 + ( z - 1 ) 2 = 5
D. ( x - 3 ) 2 + ( y + 3 ) 2 + ( z - 1 ) 2 = 5
Trong không gian với hệ tọa độ Oxyz cho u → = ( 1 ; 0 ; 1 ) v → = ( 0 ; 1 ; - 2 ) là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(-1;-1;0), B(3;1;-1). Điểm M thuộc trục Oy và cách đều hai điểm A, B có tọa độ là:

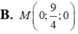
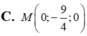

Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) có tâm I(3;-3;1) và đi qua điểm A(5;-2;1) có phương trình là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-3;1) và đường thẳng d : x + 1 2 = y + 2 − 1 = z 2 . Tìm tọa độ điểm M’ đối xứng với M qua d.
A. M'(3;-3;0)
B. M'(1;-3;2)
C. M'(0;-3;3)
D. M'(-1;-2;0)