Đáp án A
Ta có:
B A → = − 6 ; − 7 ; − 3
B C → = − m − 4 ; − m − 11 ; m + 7
Mặt khác: B A → . B C → = 0 nên m = − 4 .
Đáp án A
Ta có:
B A → = − 6 ; − 7 ; − 3
B C → = − m − 4 ; − m − 11 ; m + 7
Mặt khác: B A → . B C → = 0 nên m = − 4 .
Tìm giá trị của tham số m để đồ thị hàm số y=x4-2(m+1)x2+2m+3 có 3 điểm cực trị A,B,C là ba đỉnh của một tam giác, trục hoành chia tam gíac ABC thành một tam giác và một hình thang sao cho tỉ số diện tích tam giác nhỏ được chia ra và diện tích tam giác ABC bằng 4/9
![]()
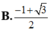
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M = 3 ; 2 ; 8 , N 0 ; 1 ; 3 và P = 2 ; m ; 4 . Tìm m để tam giác MNP vuông tại N.
A. m = 25.
B. m = 4
C. m = - 1
D. m = - 10
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(3;2;8), N(0;1;3) và P(2;m;4). Tìm m để tam giác MNP vuông tại N.
A. m=25
B. m=4
C. m=-1
D. m=-10
Trong không gian Oxyz, cho đường thẳng d : x + 1 2 = y 1 = z - 2 - 1 và hai điểm A - 1 ; 3 ; 1 ' B 0 , 2 , - 1 . Gọi C(m;n;p) là điểm thuộc d sao cho diện tích của tam giác ABC bằng 2 2 . Giá trị của tổng m + n + p bằng
A. - 1
B. 2
C. 3
D. - 5
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;-2;0), B(-3;2;-4) và mặt phẳng P : x + 2 y + z − 3 = 0 . Gọi M(a,b,c) là điểm thuộc mặt phẳng (P) sao cho tam giác MAB cân tại M và có diện tích nhỏ nhất. Tính giá trị T = a 2 + b + c .
A. T = 1.
B. T = 2.
C. T = 0.
D. T = 3.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(3;2;8), N(0;1;3), P(2;m;4). Tìm m để tam giác MNP vuông tại N.
A. m = 25
B. m = 4
C. m = -1
D. m = -10
Trong không gian Oxyz, cho hai điểm A(1;2;−3),B(−2;−2;1) và mặt phẳng α :2x+2y-z+9=0. Xét điểm M thuộc (α) sao cho tam giác AMB vuông tại M và độ dài đoạn thẳng MB đạt giá trị lớn nhất. Phương trình đường thẳng MB là
A. x = - 2 - t y = - 2 + 2 t z = 1 + 2 t
B. x = - 2 + 2 t y = - 2 - t z = 1 + 2 t
C. x = - 2 + t y = - 2 z = 1 + 2 t
D. x = - 2 + t y = - 2 - t z = 1
Trong không gian Oxyz, cho điểm M(4;6;3). Qua M kẻ các tia Mx,My,Mz đôi một vuông góc. Ba điểm A,B,C lần lượt di động trên các tia Mx,My,Mz (không trùng với điểm M) sao cho điểm G(2; 10 3 ;3) là trọng tâm tam giác ABC. Biết rằng I(a;b;c) là tâm mặt cầu ngoại tiếp tứ diện MABC. Giá trị biểu thức a+b+c bằng
A. 6.
B. 11.
C. 20.
D. 15.
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng P : x + y - z + 2 = 0 và hai điểm A 7 ; - 4 ; - 3 , B 3 ; 4 ; 1 . Gọi M a ; b ; c là điểm thuộc P a < 2 sao cho tam giác AMB vuông tại M và có diện tích nhỏ nhất. Giá trị của biểu thức 3 a + 9 b + 63 c bằng
A. 140
B. -38
C. 154
D. -21