Trong không gian Oxyz, cho mặt phẳng P : 2 x + 2 y − z + 4 = 0 và các điểm A 2 ; 1 ; 2 , B 3 ; − 2 ; 2 . Điểm M thuộc mặt phẳng (P) sao cho các đường thẳng MA, MB luôn tạo với mặt phẳng (P) một góc bằng nhau. Biết rằng điểm M luôn thuộc đường tròn (C) cố định. Tìm tọa độ tâm của đường tròn (C).
A. 74 27 ; − 97 27 ; 62 27
B. 32 9 ; − 49 9 ; 2 9
C. 10 3 ; − 3 ; 14 3
D. 17 21 ; − 17 21 ; 17 21

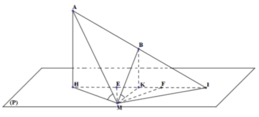
Lấy I đối xứng H qua K; E thuộc đoạn HK sao cho HE = 2KE; F thuộc đoạn KI sao cho FI = 2KF.
Khi đó: A, B, I, H, E, K, F đều là các điểm cố định.
* Ta chứng minh: M di chuyển trên đường tròn tâm F, đường kính IE: