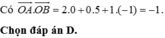Các câu hỏi tương tự
Trong không gian Oxyz, cho hai điểm A(1;−2;3), B(0;1;2). Đường thẳng d đi qua hai điểm A, B có một véctơ chỉ phương là A.
u
1
→
1
;
3
;
1
B.
u...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;−2;3), B(0;1;2). Đường thẳng d đi qua hai điểm A, B có một véctơ chỉ phương là
A. u 1 → = 1 ; 3 ; 1
B. u 2 → = 1 ; - 1 ; - 1
C. u 3 → = 1 ; - 1 ; 5
D. u 4 → = 1 ; - 3 ; 1
Trong không gian Oxyz, tích vô hướng của hai vectơ
a
→
3
;
2
;
1
và
b
→
-
5
;
2
;
-
4
bằng A. -10. B. -15 C....
Đọc tiếp
Trong không gian Oxyz, tích vô hướng của hai vectơ a → = 3 ; 2 ; 1 và b → = - 5 ; 2 ; - 4 bằng
A. -10.
B. -15
C. 15.
D. -7
Trong không gian với hệ trục tọa độ Oxyz, cho véctơ
a
→
1
;
−
2
;
3
.
Tìm tọa độ của véctơ
b
→
biết rằng véctơ
b
→
ngược hướng với véctơ
a
→
và
b
→...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho véctơ a → = 1 ; − 2 ; 3 . Tìm tọa độ của véctơ b → biết rằng véctơ b → ngược hướng với véctơ a → và b → = 2 a →
A. b → = 2 ; − 2 ; 3
B. b → = 2 ; − 4 ; 6
C. b → = − 2 ; 4 ; − 6
D. b → = − 2 ; − 2 ; 3
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(1;2;-1),B(2;0;1),C(-2;2;3). Đường thẳng
Δ
nằm trong mặt phẳng (ABC) qua trực tâm H của tam giác ABC và cùng tạo với các đường thẳng AB, AC một góc
α
45
°
có một véctơ chỉ phương là
u
→
(a;b;c) với c là một số nguyên tố. Giá trị của biểu thức ab+bc+ca bằng A. -67. B. 23. B. -33. B. -37.
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(1;2;-1),B(2;0;1),C(-2;2;3). Đường thẳng Δ nằm trong mặt phẳng (ABC) qua trực tâm H của tam giác ABC và cùng tạo với các đường thẳng AB, AC một góc α < 45 ° có một véctơ chỉ phương là u → (a;b;c) với c là một số nguyên tố. Giá trị của biểu thức ab+bc+ca bằng
A. -67.
B. 23.
B. -33.
B. -37.
Trong không gian Oxyz, cho hai điểm A(1;−2;1), B(0;1;−3). Toạ độ véctơ A B ⇀ là
A. (1;-3;4)
B. (1;-1;2)
C. (-1;3;-4)
D. (-1;1;2)
Trong không gian Oxyz, cho
a
→
3
;
0
;
-
6
,
b
→
2
;
-
4
;
0
. Tích vô hướng của vectơ
a
→
và...
Đọc tiếp
Trong không gian Oxyz, cho a → = 3 ; 0 ; - 6 , b → = 2 ; - 4 ; 0 . Tích vô hướng của vectơ a → và b → bằng:
A. 6
B. -4
C. 0
D. -6
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-2;3), B(2;0;1), C(3;-1;5). Diện tích tam giác ABC là:
A. 3 2
B. 7 2
C. 5 2
D. 9 2
Trong không gian Oxyz, phương trình mặt phẳng (P) đi qua hai điểm A(1;-7;-8), B(2;-5;-9) sao cho khoảng cách từ điểm M(7;-1;-2) đến (P) lớn nhất có một véctơ pháp tuyến là
n
→
(a;b;4). Giá trị của tổng a+b là A. -1. B. 3 C. 6 D. 2
Đọc tiếp
Trong không gian Oxyz, phương trình mặt phẳng (P) đi qua hai điểm A(1;-7;-8), B(2;-5;-9) sao cho khoảng cách từ điểm M(7;-1;-2) đến (P) lớn nhất có một véctơ pháp tuyến là n → =(a;b;4). Giá trị của tổng a+b là
A. -1.
B. 3
C. 6
D. 2
Trong không gian Oxyz, cho 2 véc tơ
a
→
(
1
;
-
5
;
2
)
,
b
→
(
2
;
-
4
;
0
)
Tính tích vô hướng của 2 véc tơ
a
→
và
b
→
. A. ...
Đọc tiếp
Trong không gian Oxyz, cho 2 véc tơ a → ( 1 ; - 5 ; 2 ) , b → ( 2 ; - 4 ; 0 ) Tính tích vô hướng của 2 véc tơ a → và b → .
A. a → . b → = - 22
B. a → . b → = 22
C. a → . b → = 11
D. a → . b → = - 11